《2022年中考數(shù)學(xué)專題復(fù)習(xí)小訓(xùn)練 專題11 反比例函數(shù)》由會員分享，可在線閱讀，更多相關(guān)《2022年中考數(shù)學(xué)專題復(fù)習(xí)小訓(xùn)練 專題11 反比例函數(shù)（3頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

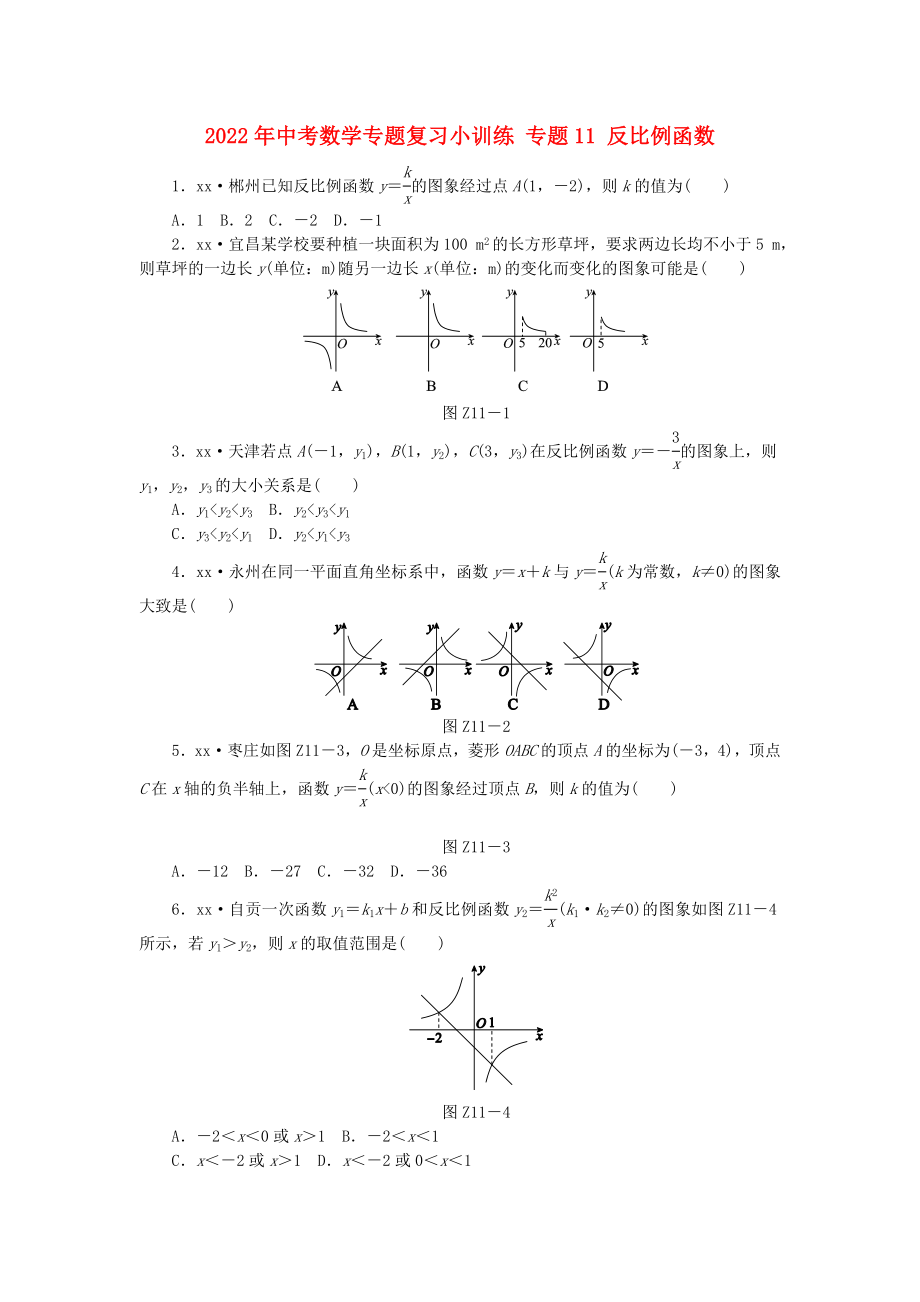
1、2022年中考數(shù)學(xué)專題復(fù)習(xí)小訓(xùn)練 專題11 反比例函數(shù) 1．xx·郴州已知反比例函數(shù)y＝的圖象經(jīng)過點(diǎn)A(1，－2)，則k的值為(　　) A．1 B．2 C．－2 D．－1 2．xx·宜昌某學(xué)校要種植一塊面積為100 m2的長方形草坪，要求兩邊長均不小于5 m，則草坪的一邊長y(單位：m)隨另一邊長x(單位：m)的變化而變化的圖象可能是(　　) 圖Z11－1 3．xx·天津若點(diǎn)A(－1，y1)，B(1，y2)，C(3，y3)在反比例函數(shù)y＝－的圖象上，則y1，y2，y3的大小關(guān)系是(　　) A．y1

2、

3、C．x＜－2或x＞1 D．x＜－2或0＜x＜1 7．xx·福建A卷如圖Z11－5，直線y＝x＋m與雙曲線y＝交于A，B兩點(diǎn)，作BC∥x軸，AC∥y軸，交于點(diǎn)C，則S△ABC的最小值是________． 圖Z11－5 8．xx·天門如圖Z11－6，在平面直角坐標(biāo)系中，直線y＝－x與反比例函數(shù)y＝(k≠0)在第二象限內(nèi)的圖象相交于點(diǎn)A(m，1)． (1)求反比例函數(shù)的表達(dá)式； (2)將直線y＝－x向上平移后與反比例函數(shù)在第二象限內(nèi)的圖象交于點(diǎn)B，與y軸交于點(diǎn)C，且△ABO的面積為，求直線BC的表達(dá)式． 圖Z11－6 詳解詳析 1．C　2.C　3.B　4.B

4、　5.C　6.D 7．6　[解析] ∵直線y＝x＋m與y＝x平行， ∴AC＝BC，∴S△ABC＝BC2. 將y＝x＋m與y＝聯(lián)立，得方程組 整理，得x2＋mx－3＝0， ∴x1＋x2＝－m，x1·x2＝－3. ∵BC＝xA－xB＝|x1－x2|， ∴|x1－x2|＝＝， ∴S△ABC＝BC2＝(m2＋12)＝m2＋6， ∴S△ABC的最小值是6. 8．解：(1)∵直線y＝－x過點(diǎn)A(m，1)， ∴－m＝1， 解得m＝－2， ∴A(－2，1)． ∵反比例函數(shù)y＝(k≠0)的圖象過點(diǎn)A(－2，1)， ∴k＝－2×1＝－2，∴反比例函數(shù)的表達(dá)式為y＝－. (2)設(shè)直線BC的表達(dá)式為y＝－x＋b，連接AC， ∵△ACO與△ABO的面積相等，且△ABO的面積為， ∴△ACO的面積＝OC·2＝， ∴OC＝，∴b＝， ∴直線BC的表達(dá)式為y＝－x＋.