《版高考數(shù)學二輪復習分層設計全國通用第二層提升篇：課件 專題一 第2講　三角恒等變換與解三角形》由會員分享，可在線閱讀，更多相關《版高考數(shù)學二輪復習分層設計全國通用第二層提升篇：課件 專題一 第2講　三角恒等變換與解三角形（45頁珍藏版）》請在裝配圖網(wǎng)上搜索。

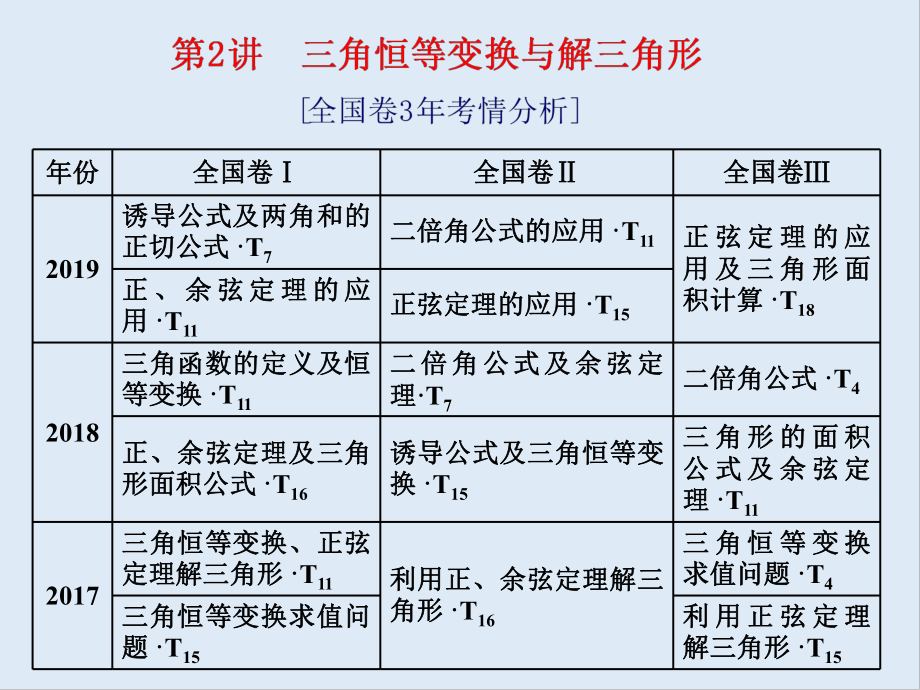
1、年份年份全國卷全國卷全國卷全國卷全國卷全國卷2019誘導公式及兩角和的誘導公式及兩角和的正切公式正切公式T7二倍角公式的應用二倍角公式的應用T11正 弦 定 理 的 應正 弦 定 理 的 應用 及 三 角 形 面用 及 三 角 形 面積計算積計算T18正、余弦定理的應正、余弦定理的應用用T11正弦定理的應用正弦定理的應用T152018三角函數(shù)的定義及恒三角函數(shù)的定義及恒等變換等變換T11二倍角公式及余弦定二倍角公式及余弦定理理T7二倍角公式二倍角公式T4正、余弦定理及三角正、余弦定理及三角形面積公式形面積公式T16誘導公式及三角恒等變誘導公式及三角恒等變換換T15三 角 形 的 面 積三 角

2、形 的 面 積公 式 及 余 弦 定公 式 及 余 弦 定理理T112017三角恒等變換、正弦三角恒等變換、正弦定理解三角形定理解三角形T11利用正、余弦定理解三利用正、余弦定理解三角形角形T16三 角 恒 等 變 換三 角 恒 等 變 換求值問題求值問題T4三角恒等變換求值問三角恒等變換求值問題題T15利 用 正 弦 定 理利 用 正 弦 定 理解三角形解三角形T15給角給角求值求值解決給角求值問題的關鍵是兩種變換：一是角的變換，解決給角求值問題的關鍵是兩種變換：一是角的變換，注意各角之間是否具有和差關系、互補注意各角之間是否具有和差關系、互補(余余)關系、倍關系、倍半關系，從而選擇相應公式

3、進行轉化，把非特殊角的半關系，從而選擇相應公式進行轉化，把非特殊角的三角函數(shù)相約或相消，從而轉化為特殊角的三角函數(shù)；三角函數(shù)相約或相消，從而轉化為特殊角的三角函數(shù)；二是結構變換，在熟悉各種公式的結構特點、符號特二是結構變換，在熟悉各種公式的結構特點、符號特征的基礎上，結合所求式子的特點合理地進行變形征的基礎上，結合所求式子的特點合理地進行變形給值給值求值求值給值求值的關鍵是找出已知式與待求式之間的聯(lián)系及給值求值的關鍵是找出已知式與待求式之間的聯(lián)系及函數(shù)的差異，一般可以適當變換已知式，求得另外某函數(shù)的差異，一般可以適當變換已知式，求得另外某些函數(shù)式的值，以備應用同時也要注意變換待求式，些函數(shù)式的

4、值，以備應用同時也要注意變換待求式，便于將已知式求得的函數(shù)值代入，從而達到解題的目便于將已知式求得的函數(shù)值代入，從而達到解題的目的的給值給值求角求角實質上也轉化為實質上也轉化為“給值求值給值求值”，關鍵也是變角，把所，關鍵也是變角，把所求角用含已知角的式子表示，由所得的函數(shù)值結合該求角用含已知角的式子表示，由所得的函數(shù)值結合該函數(shù)的單調區(qū)間求得角，有時要壓縮角的取值范圍函數(shù)的單調區(qū)間求得角，有時要壓縮角的取值范圍(單擊進入電子文檔單擊進入電子文檔)求什么求什么想什么想什么求角求角B的大小，想到角的大小，想到角B的三角函數(shù)值的三角函數(shù)值求三角函數(shù)值，想到由已知三角函數(shù)值求值求三角函數(shù)值，想到由已知三角函數(shù)值求值給什么給什么用什么用什么已知邊角關系式，用正弦定理統(tǒng)一角已知邊角關系式，用正弦定理統(tǒng)一角已知邊的大小，用余弦定理求邊已知邊的大小，用余弦定理求邊.差什么差什么找什么找什么求求sin(2AB)的值，缺少的值，缺少2A的三角函數(shù)值，的三角函數(shù)值，應找應找A的三角函數(shù)值的三角函數(shù)值.謝觀看THANK YOU FOR WATCHING謝