《人教版九下數(shù)學(xué) 第二十七章 方法技巧專(zhuān)題二 方法技巧7 作垂線(xiàn)構(gòu)造直角三角形相似》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《人教版九下數(shù)學(xué) 第二十七章 方法技巧專(zhuān)題二 方法技巧7 作垂線(xiàn)構(gòu)造直角三角形相似（4頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

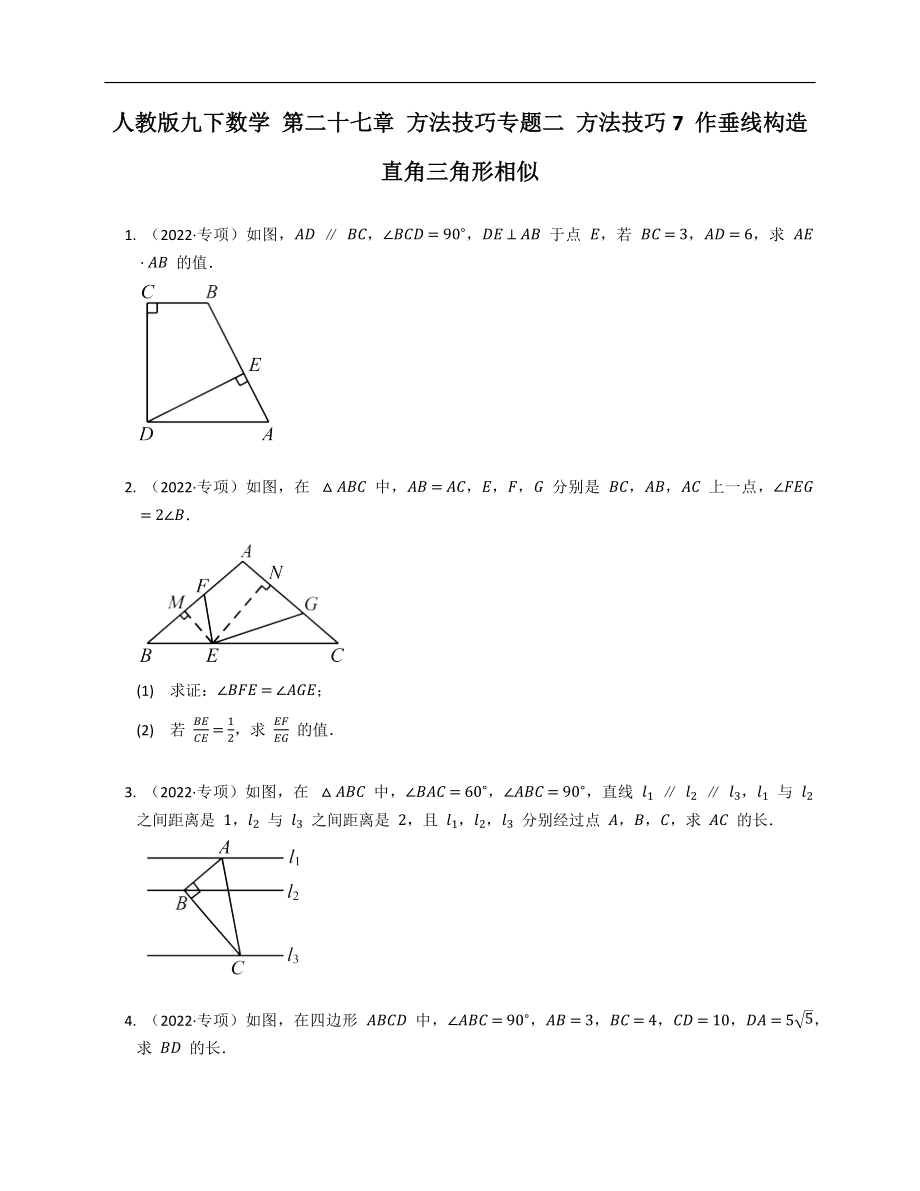
1、 人教版九下數(shù)學(xué) 第二十七章 方法技巧專(zhuān)題二 方法技巧7 作垂線(xiàn)構(gòu)造直角三角形相似 1. （2022·專(zhuān)項(xiàng)）如圖，AD∥BC，∠BCD=90°，DE⊥AB 于點(diǎn) E，若 BC=3，AD=6，求 AE?AB 的值． 2. （2022·專(zhuān)項(xiàng)）如圖，在 △ABC 中，AB=AC，E，F(xiàn)，G 分別是 BC，AB，AC 上一點(diǎn)，∠FEG=2∠B． (1) 求證：∠BFE=∠AGE； (2) 若 BECE=12，求 EFEG 的值． 3. （2022·專(zhuān)項(xiàng)）如圖，在 △ABC 中，∠BAC=60°，∠ABC=90°，直線(xiàn) l1∥l2∥l3，l1 與 l2 之間距離是

2、 1，l2 與 l3 之間距離是 2，且 l1，l2，l3 分別經(jīng)過(guò)點(diǎn) A，B，C，求 AC 的長(zhǎng)． 4. （2022·專(zhuān)項(xiàng)）如圖，在四邊形 ABCD 中，∠ABC=90°，AB=3，BC=4，CD=10，DA=55，求 BD 的長(zhǎng)． 答案 1. 【答案】作 BG⊥AD 于點(diǎn) G，△ABG∽△ADE， ∴AE?AB=AD?AG=6×3=18． 【知識(shí)點(diǎn)】?jī)山欠謩e相等 2. 【答案】 (1) ∵ 2∠B+∠A=180°， ∴ ∠FEG+∠A=180°， ∴ ∠BFE=∠AGE． (2) 過(guò) E 作 EM⊥AB 于 M，作 EN⊥AC 于 N

3、， ∴ △EMF∽△ENG， ∴ EFEG=EMEN，易證 △EBM∽△ECN， ∴ EMEN=BECE=12， ∴ EFEG=12． 【知識(shí)點(diǎn)】?jī)山欠謩e相等、兩邊成比例且?jiàn)A角相等、等邊對(duì)等角 3. 【答案】過(guò)點(diǎn) B 作 MN⊥l2，交 l1 于點(diǎn) N，交 l3 于點(diǎn) M， 則 △NAB∽△MBC， ∴NAMB=ABBC=33， ∴NA=233， ∴BA=NB2+NA2=213， ∴AC=2BA=2321． 【知識(shí)點(diǎn)】?jī)山欠謩e相等、勾股定理、對(duì)應(yīng)邊成比例 4. 【答案】解法一： 連接 AC，過(guò)點(diǎn) B 作 BE⊥CD 于點(diǎn) E， AC=5，易證 AC2+CD2=AD2， ∴∠ACD=90°，易證 △ABC∽△CEB， ∴ABCE=BCEB=ACCB， ∴3CE=4BE=54， ∴CE=125，EB=165， ∴BD=BE2+DE2=241． 【解析】解法二： 易證 ∠ACD=90°，作 DF⊥BC 于點(diǎn) F， ∴△DCF∽△CAB， ∴CFAB=DFBC=CDAC=105=2， ∴CF=6，DF=8， ∴BD=BF2+DF2=241． 【知識(shí)點(diǎn)】?jī)山欠謩e相等