《高三數(shù)學(xué)概率與統(tǒng)計(jì)-正態(tài)分布》由會(huì)員分享�����,可在線閱讀��,更多相關(guān)《高三數(shù)學(xué)概率與統(tǒng)計(jì)-正態(tài)分布(9頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
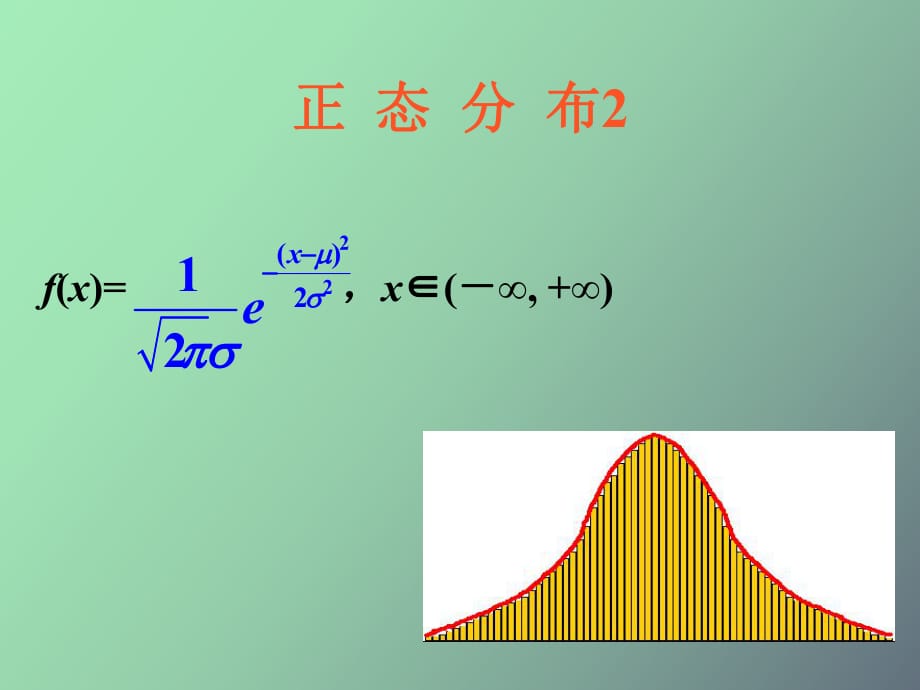
1���、正 態(tài) 分 布 222( )212 xe f(x)= , x ( , +) 標(biāo) 準(zhǔn) 正 態(tài) 曲 線 :當(dāng) =0���、 =l時(shí) ��, 正 態(tài) 總 體 稱 為����, 其 相 應(yīng) 的 函 數(shù) 表 示 式 是 )( 21)( 22 xexf x其 相 應(yīng) 的 曲 線 稱 為 Oy x x0 x1 x2x0 xOy正 態(tài) 分 布 表 中 ����, 相 應(yīng) 于 x0的 值 (x0)是 指 總 體 取 值 小 于 x0的 概 率��, 用 圖 形 表 示 為 (陰 影 部 分 面 積 ) 說 明 :(1) (2)標(biāo) 準(zhǔn) 正 態(tài) 總 體 在 任 一 區(qū) 間 (x1, x2)內(nèi) 取值 的 概 率(3)對(duì) 任 一 正 態(tài) 總 體 N
2�����、(,2)��, 取 值 小 于 x的 概 率 )()( xxF即 ���, 若 服 從 正 態(tài) 分 布 N(,2), 則 服 從 標(biāo) 準(zhǔn) 正 態(tài) 分 布 例 1. 若 x N(0,1),求 (l)P(2.32x1.2)��; (2)P(x2).解 : (1)P(2.32x1.2)=(1.2)(2.32) =(1.2)1(2.32)=0.8849(10.9898)=0.8747. (2)P(x2)=1P(x2)=1(2)=l0.9772=0.0228.例2:已知正態(tài)總體 , 求取值小于3的概率. )4,1(N .8413.012 133 F 例 3:分 別 求 正 態(tài) 總 體 在 區(qū) 間 : 內(nèi) 取 值 的
3����、概 率 . 2,N 、 , �����、 2,2 ���、 3,3 1 F 1 F所以�����,正態(tài)總體 在區(qū)間: 內(nèi)取值的概率是: 2,N �����、 , 11211 FF ;683.018413.02 解: 例 3:分 別 求 正 態(tài) 總 體 在 區(qū) 間 : 內(nèi) 取 值 的 概 率 . 2,N ��、 , �����、 2,2 �����、 3,3 954.02222 FF解: 同理��,正態(tài)總體 在區(qū)間: 內(nèi)取值的概率是: 2,N ��、 2,2 正態(tài)總體 在區(qū)間: 內(nèi)取值的概率是: 2,N ���、 3,3 .997.03333 FF 上述計(jì)算結(jié)果可用下表和圖來表示: 區(qū) 間 取 值 概 率 , 2,2 3,3 oo3.68 oo4.95 oo7.99 小概率事件的含義: 我們從上圖看到,正態(tài)總體在 以外取值的概率只有4.6����,在 以外取值的概率只有0.3 ����。 2,2 3,3 由于這些概率值很?���。ㄒ话悴怀^5 ),通常稱這些情況發(fā)生為小概率事件�����。即事件在一次試驗(yàn)中幾乎不可能發(fā)生�����。 例4:某校高中二年級(jí)期末考試的數(shù)學(xué)成績N(7,102).若參加考試的學(xué)生有100人,學(xué)生甲得分為80分,求學(xué)生甲的數(shù)學(xué)成績排名;若及格(60分及其以上)的學(xué)生有101人,求第20名的數(shù)學(xué)成績.
 高三數(shù)學(xué)概率與統(tǒng)計(jì)-正態(tài)分布
高三數(shù)學(xué)概率與統(tǒng)計(jì)-正態(tài)分布