《浙江省2018年中考數(shù)學(xué)復(fù)習(xí) 第二部分 題型研究 題型一 數(shù)學(xué)思想方法 類型五 整體思想針對演練》由會員分享�����,可在線閱讀�����,更多相關(guān)《浙江省2018年中考數(shù)學(xué)復(fù)習(xí) 第二部分 題型研究 題型一 數(shù)學(xué)思想方法 類型五 整體思想針對演練(5頁珍藏版)》請在裝配圖網(wǎng)上搜索�����。
1�����、
第二部分 題型研究
題型一 數(shù)學(xué)思想方法
類型五 整體思想
針對演練
1. 已知:a-b=�����,b-c=�����,a2+b2+c2=1�����,則ab+bc+ca的值等于________.
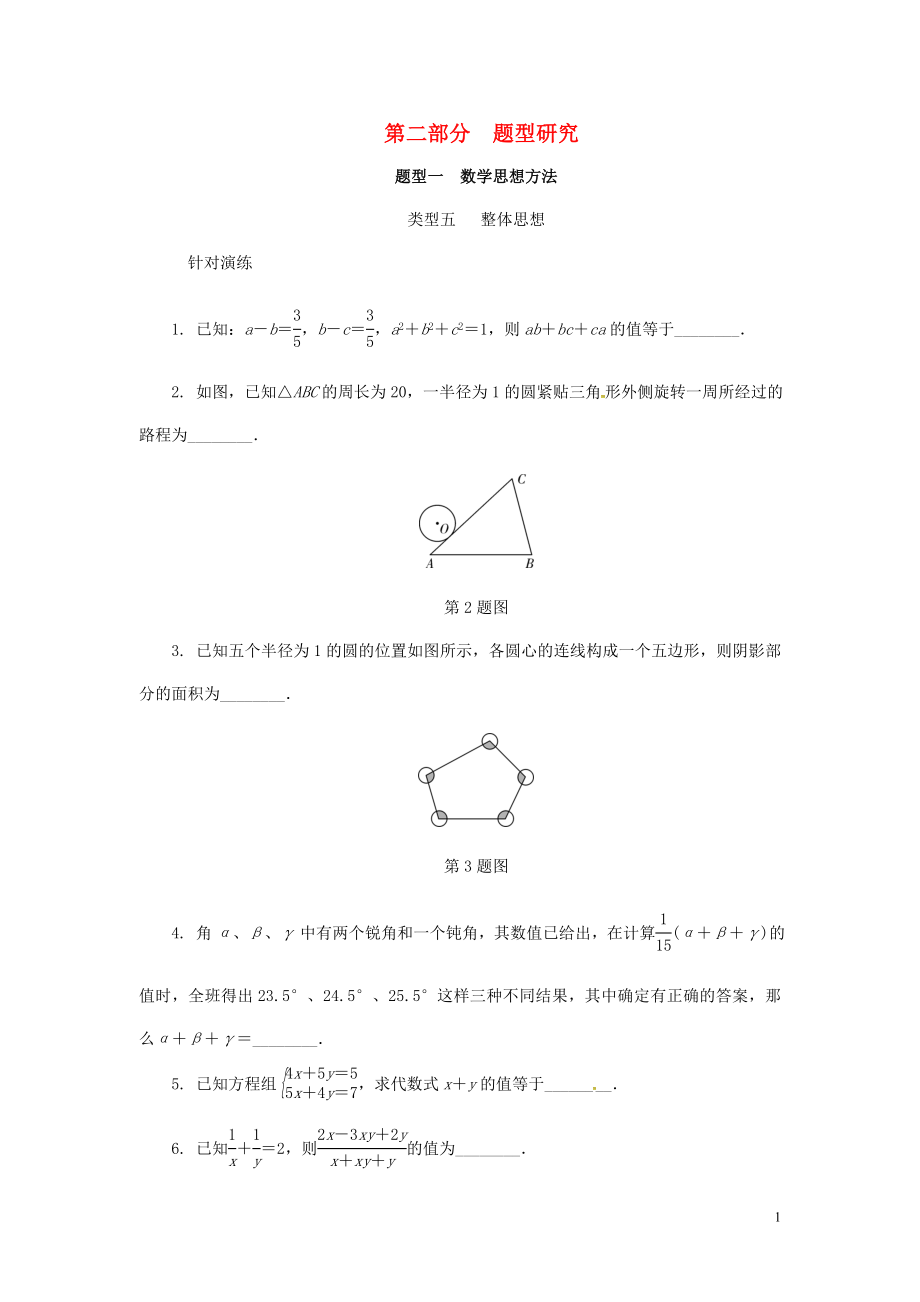
2. 如圖�����,已知△ABC的周長為20�����,一半徑為1的圓緊貼三角形外側(cè)旋轉(zhuǎn)一周所經(jīng)過的路程為________.
第2題圖
3. 已知五個半徑為1的圓的位置如圖所示�����,各圓心的連線構(gòu)成一個五邊形�����,則陰影部分的面積為________.
第3題圖
4. 角α�����、β�����、γ中有兩個銳角和一個鈍角,其數(shù)值已給出�����,在計算(α+β+γ)的值時�����,全班得出23.5°�����、24.5°�����、25.5°這樣三種不同結(jié)果�����,其中確定有正
2�����、確的答案,那么α+β+γ=________.
5. 已知方程組�����,求代數(shù)式x+y的值等于________.
6. 已知+=2�����,則的值為________.
7. 計算(1----)(++++)-(1-----)(+++)的結(jié)果是________.
8. 如圖�����,已知Rt△ABC的周長為2+�����,其中AB=2�����,則這個三角形的面積是________.
第8題圖
9. 如圖�����,△ABC中�����,AC=8�����,BC=5�����,AB的垂直平分線DE交AB于點D�����,交邊AC于點E�����,則△BCE的周長為________.
第9題圖
10. 分解因式:(x2-3x+2)(x2-3x-4)-72.
3�����、
11. 有甲�����、乙、丙三種貨物�����,若購甲3件�����,乙7件�����,丙1件�����,共需3.15元�����;若購甲4件�����,乙10件�����,丙1件�����,共需4.20元.
現(xiàn)在計劃購甲�����、乙�����、丙各1件�����,共需多少元�����?
12. 如圖�����,矩形ABCD中,AB=6�����,AD=8�����,P是BC上一點�����,PE⊥BD于E�����,PF⊥AC于F�����,求PE+PF的長.
第12題圖
答案
1. - 【解析】可將ab+bc+ca當作整體去求解�����,不用分別求出a�����、b�����、c的值.∵a-b=�����,b-c=�����,∴a-c=�����,則有(a-b)2+(b-c)2+(c-a)2=�����,即a2+b2+c2-ab-bc-ac=�����,又∵a2+b2+c2=1,∴ab+bc+ac=-.
2. 20+2π 【解
4�����、析】⊙O在△ABC的三個頂點處所轉(zhuǎn)過的圓心角度數(shù)和為360°×3-90°×2×3-180°=360°.所以總長度為L=20+2π.
3. 【解析】將五個扇形的圓心角度和作為整體�����,∵五個扇形的圓心角的和=(5-2)×180°=540°�����,r=1�����,
∴S陰影部分==.
4. 352.5° 【解析】將a+β+r看作整體.設(shè)0°<α<90°�����,0°<β<90°�����,90°<γ<180°�����,∴90°<α+β+γ<360°�����,∴6°<(α+β+γ)<24°.∵23.5°�����、24.5°�����、25.5°中有正確答案�����,∴(α+β+γ)=23.5°�����,∴α+β+γ=352.5°.
5. 【解析】將(x+y)作為整體�����,
5、方程組中的兩個方程相加得:9x+9y=12�����,∴9(x+y)=12�����,即x+y=.
6. 【解析】∵+=2�����,∴x+y=2xy�����,∴===.
7. 【解析】設(shè)+++=a�����,則原式=(1-a)·(a+)-(1-a-)a=+a-a2-a+a2=.
8. 【解析】在Rt△ABC中�����,根據(jù)勾股定理�����,得a2+b2=22�����,即(a+b)2-2ab=4�����,又∵a+b=�����,∴()2-2ab=4�����,∴ab=1�����,∴S=ab=.
9. 13 【解析】∵DE是AB的垂直平分線�����,∴EA=EB,則△BCE的周長=BC+EC+EB=BC+EC+EA=BC+AC=13.
10. 解:設(shè)x2-3x=a�����,
則原式=(a+2)(
6�����、a-4)-72
=a2-2a-80
=(a-10)(a+8)
=(x2-3x-10)(x2-3x+8)
=(x-5)(x+2)(x2-3x+8).
11.解:設(shè)甲�����、乙�����、丙三種貨物的單價各為x�����、y�����、z元�����,
由題意可得:3x+7y+z=3.15?����、?����,
4x+10y+z=4.20?����、?����,
三個未知數(shù)�����,2個方程�����,故考慮將x+y+z當作整體來解答.
②-①得x+3y=1.05 ③�����,
③×3得3x+9y=3.15?����、?����,
②-④得x+y+z=1.05�����,
答:購甲�����、乙�����、丙各1件,共需1.05元.
12. 解:由已知條件并不能求得PE�����、PF的長�����,我們把PE+PF的值看成一個整體.由題設(shè)條件可知:△BPE∽△BDC�����,
∴=�����,
∵△CPF∽△CAB�����,
∴=�����,
又∵四邊形ABCD為矩形�����,
∴AB=DC=6�����,AC=BD===10�����,
∴==�����,
∴PE+PF=4.8.
5
 浙江省2018年中考數(shù)學(xué)復(fù)習(xí) 第二部分 題型研究 題型一 數(shù)學(xué)思想方法 類型五 整體思想針對演練
浙江省2018年中考數(shù)學(xué)復(fù)習(xí) 第二部分 題型研究 題型一 數(shù)學(xué)思想方法 類型五 整體思想針對演練