《甘肅省2019年中考數(shù)學(xué)總復(fù)習(xí) 第六單元 圓 考點強化練22 與圓有關(guān)的計算練習(xí)》由會員分享，可在線閱讀，更多相關(guān)《甘肅省2019年中考數(shù)學(xué)總復(fù)習(xí) 第六單元 圓 考點強化練22 與圓有關(guān)的計算練習(xí)（12頁珍藏版）》請在裝配圖網(wǎng)上搜索。

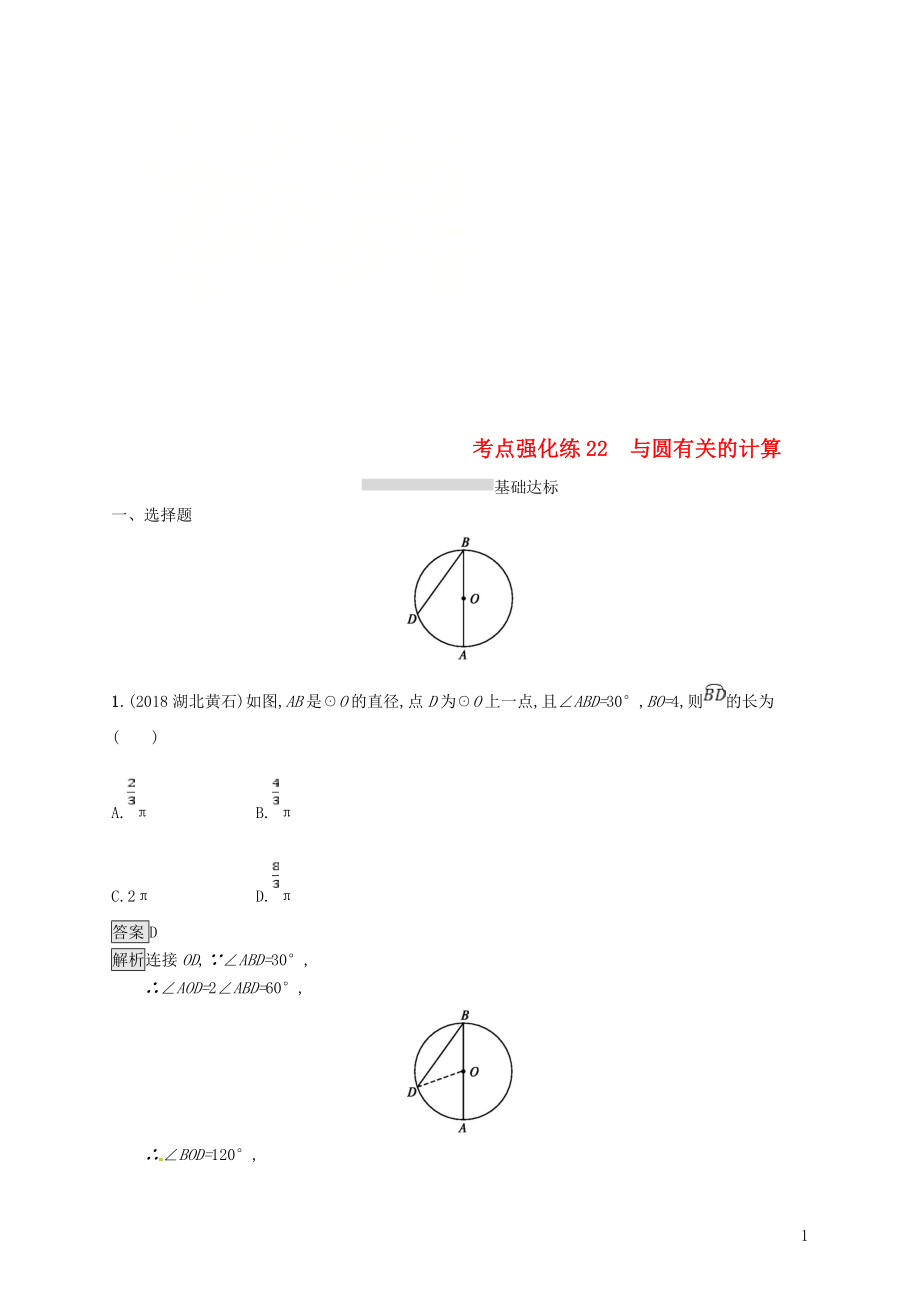
1、 考點強化練22　與圓有關(guān)的計算 基礎(chǔ)達(dá)標(biāo) 一、選擇題 1.(2018湖北黃石)如圖,AB是☉O的直徑,點D為☉O上一點,且∠ABD=30°,BO=4,則的長為(　　) A.π B.π C.2π D.π 答案D 解析連接OD,∵∠ABD=30°, ∴∠AOD=2∠ABD=60°, ∴∠BOD=120°, ∴的長=,故選D. 2.(2018江蘇南通)一個空間幾何體的主視圖和左視圖都是邊長為2 cm的正三角形,俯視圖是一個圓,則這個幾何體的表面積是(　　) A.π cm2 B.3π cm2 C.π cm2 D.5π cm2 答案B 解析綜合主視圖,俯視圖,左

2、視圖可以看出這個幾何體應(yīng)該是圓錐,且底面圓的半徑為1,母線長為2,因此側(cè)面面積為×2×1×π×2=2π,底面積為π×12=π.表面積為2π+π=3π(cm2).故選B. 3.(2018山東德州)如圖,從一塊直徑為2 m的圓形鐵皮上剪出一個圓心角為90°的扇形,則此扇形的面積為(　　) A. m2 B.π m2 C.π m2 D.2π m2 答案A 解析連接AC(圖略). ∵從一塊直徑為2 m的圓形鐵皮上剪出一個同心角為90°的扇形,即∠ABC=90°, ∴AC為直徑,即AC=2 m,AB=BC. ∵AB2+BC2=22,∴AB=BC= m, ∴陰影部分的面積是π(m2).

3、故選A. 4.(2018四川成都)如圖,在?ABCD中,∠B=60°,☉C的半徑為3,則圖中陰影部分的面積是(　　) A.π B.2π C.3π D.6π 答案C 解析∵在?ABCD中,∠B=60°,☉C的半徑為3,∴∠C=120°,∴圖中陰影部分的面積是=3π,故選C. 5.在半徑為6 cm的圓中,長為2π cm的弧所對的圓心角的度數(shù)是(　　) A.30° B.45° C.60° D.90° 答案C 解析由弧長公式得2π=,解得n=60.故選C. 6.(2018四川自貢)已知圓錐的側(cè)面積是8π cm2,若圓錐底面半徑為R(cm),母線長為l(cm),則R關(guān)于l的函數(shù)圖

4、象大致是(　　) 答案A 解析由題意得,×2πR×1=8π,則R=,故選A. 7.如圖,AB是☉O的切線,B為切點,AC經(jīng)過點O,與☉O分別相交于點D,C.若∠ACB=30°,AB=,則陰影部分的面積是 (　　) A. B. C. D. 答案C 解析連接OB.∵AB是☉O的切線,∴OB⊥AB, ∵OC=OB,∠C=30°, ∴∠C=∠OBC=30°, ∴∠AOB=∠C+∠OBC=60°,在Rt△ABO中, ∵∠ABO=90°,AB=,∠A=30°,∴OB=1, ∴S陰影=S△ABO-S扇形OBD=×1×.故選C. 8.如圖,矩形ABCD中,AB=5,AD=

5、12,將矩形ABCD 按如圖所示的方式在直線l上進(jìn)行兩次旋轉(zhuǎn),則點B在兩次旋轉(zhuǎn)過程中經(jīng)過的路徑的長是(　　) A. B.13π C.25π D.25 答案A 解析如圖,連接BD,B'D,∵AB=5,AD=12, ∴BD==13. ∴. ∵=6π, ∴點B在兩次旋轉(zhuǎn)過程中經(jīng)過的路徑的長是+6π=. 9.(2018遼寧沈陽)如圖,正方形ABCD內(nèi)接于O,AB=2,則的長是(　　) A.π B.π C.2π D.π 答案A 解析連接OA,OB, ∵正方形ABCD內(nèi)接于圓O,∴AB=BC=DC=AD, ∴, ∴∠AOB=×360°=90°, 在Rt△AO

6、B中,由勾股定理得,2AO2=(2)2, 解得AO=2,∴的長為=π,故選A. 二、填空題 10.如圖所示,在3×3的方格紙中,每個小方格都是邊長為1的正方形,點O,A,B均為格點,則扇形OAB的面積大小是　　　　　.? 答案 解析∵每個小方格都是邊長為1的正方形, ∴OA=OB=, ∴S扇形OAB=. 故答案為. 11.(2018山東聊城)用一塊圓心角為216°的扇形鐵皮,做一個高為40 cm的圓錐形工件(接縫忽略不計),則這個扇形鐵皮的半徑是　　　　　 cm.? 答案50 解析設(shè)這個扇形鐵皮的半徑為R cm, 圓錐的底面圓的半徑為r cm, 根據(jù)題意得2πr=

7、,解得r=R, 因為402+=R2,解得R=50. 所以這個扇形鐵皮的半徑為50 cm. 12.(2018湖北荊門)如圖,在平行四邊形ABCD中,AB

8、題 13.(2017貴州安順)如圖,AB是☉O的直徑,C是☉O上一點,OD⊥BC于點D,過點C作☉O的切線,交OD的延長線于點E,連接BE. (1)求證:BE與☉O相切; (2)設(shè)OE交☉O于點F,若DF=1,BC=2,求陰影部分的面積. (1)證明連接OC,如圖, ∵CE為切線,∴OC⊥CE, ∴∠OCE=90°, ∵OD⊥BC,∴CD=BD, 即OD垂直平分BC, ∴EC=EB, 在△OCE和△OBE中 ∴△OCE≌△OBE,∴∠OBE=∠OCE=90°,∴OB⊥BE,∴BE與☉O相切. (2)解設(shè)☉O的半徑為r,則OD=r-1, 在Rt△OBD中,BD=

9、CD=BC=, ∴(r-1)2+()2=r2,解得r=2, ∵tan∠BOD=,∴∠BOD=60°, ∴∠BOC=2∠BOD=120°, 在Rt△OBE中,BE=OB=2, ∴陰影部分的面積=S四邊形OBEC-S扇形BOC=2S△OBE-S扇形BOC=2××2×2=4π. 14.如圖,在平面直角坐標(biāo)系xOy中,以點O為圓心的圓交x軸的正半軸于點M,交y軸的正半軸于點N.劣弧的長為π,直線y=-x+4與x軸、y軸分別交于點A,B. (1)求證:直線AB與☉O相切; (2)求圖中陰影部分的面積.(結(jié)果用π表示) (1)證明作OD⊥AB于點D,如圖所示. ∵劣弧的長為π,

10、∴π,解得:OM=, 即☉O的半徑為. ∵直線y=-x+4與x軸、y軸分別交于點A,B,當(dāng)y=0時,x=3;當(dāng)x=0時,y=4, ∴A(3,0),B(0,4),∴OA=3,OB=4, ∴AB==5. ∵△AOB的面積=AB·OD=OA·OB,∴OD==半徑OM,∴直線AB與☉O相切. (2)解圖中所示的陰影部分的面積=△AOB的面積-扇形OMN的面積=×3×4-π×=6-π. ?導(dǎo)學(xué)號13814064? 能力提升 一、選擇題 1.(2018四川廣安)如圖,已知☉O的半徑是2,點A,B,C在☉O上,若四邊形OABC為菱形,則圖中陰影部分面積為(　　) A.π-2 B

11、.π- C.π-2 D.π- 答案C 解析連接OB和AC交于點D,如圖所示, ∵圓的半徑為2, ∴OB=OA=OC=2, 又四邊形OABC是菱形, ∴OB⊥AC,OD=OB=1, 在Rt△COD中利用勾股定理可知,CD=,AC=2CD=2, ∴sin∠COD=, ∴∠COD=60°,∠AOC=2∠COD=120°, ∴S菱形ABCO=OB·AC=×2×2=2,S扇形AOC=,則圖中陰影部分面積為S扇形AOC-S菱形ABCO=π-2,故選C. 二、填空題 2.(2018湖南永州)如圖,在平面直角坐標(biāo)系中,已知點A(1,1),以點O為旋轉(zhuǎn)中心,將點A逆時針旋轉(zhuǎn)到點

12、B的位置,則的長為　　　　　.? 答案 解析∵點A(1,1),∴OA=,點A在第一象限的角平分線上,∵以點O為旋轉(zhuǎn)中心,將點A逆時針旋轉(zhuǎn)到點B的位置,∴∠AOB=45°, ∴的長為. 3.(2018廣東)如圖,在矩形ABCD中,BC=4,CD=2,以AD為直徑的半圓O與BC相切于點E,連接BD,則陰影部分的面積為　　　　　.(結(jié)果保留π)? 答案π 解析連接OE,如圖, ∵以AD為直徑的半圓O與BC相切于點E, ∴OD=2,OE⊥BC, 易得四邊形OECD為正方形, ∴由弧DE、線段EC,CD所圍成的面積=S正方形OECD-S扇形EOD=22-=4-π, ∴陰影部

13、分的面積=×2×4-(4-π)=π. 三、解答題 4.如圖,在Rt△ABC中,∠B=90°,點O在邊AB上,以點O為圓心,OA為半徑的圓經(jīng)過點C,過點C作直線MN,使∠BCM=2∠A. (1)判斷直線MN與☉O的位置關(guān)系,并說明理由; (2)若OA=4,∠BCM=60°,求圖中陰影部分的面積. 解(1)MN是☉O切線. 理由:連接OC.∵OA=OC,∴∠OAC=∠OCA, ∴∠BOC=∠A+∠OCA=2∠A,∵∠BCM=2∠A,∴∠BCM=∠BOC.∵∠B=90°, ∴∠BOC+∠BCO=90°,∴∠BCM+∠BCO=90°,∴OC⊥MN,∴MN是☉O的切線. (2)由(1)可知∠BOC=∠BCM=60°, ∴∠AOC=120°,在Rt△BCO中,OC=OA=4,∠BCO=30°, ∴BO=OC=2,BC=2, ∴S陰影=S扇形OAC-S△OAC=×4×2-4. ?導(dǎo)學(xué)號13814065? 12