《2018年九年級數(shù)學(xué)下冊 第二十七章 相似 27.2 相似三角形 27.2.1 相似三角形的判定 第3課時 邊角判定三角形相似課后作業(yè) （新版）新人教版》由會員分享，可在線閱讀，更多相關(guān)《2018年九年級數(shù)學(xué)下冊 第二十七章 相似 27.2 相似三角形 27.2.1 相似三角形的判定 第3課時 邊角判定三角形相似課后作業(yè) （新版）新人教版（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

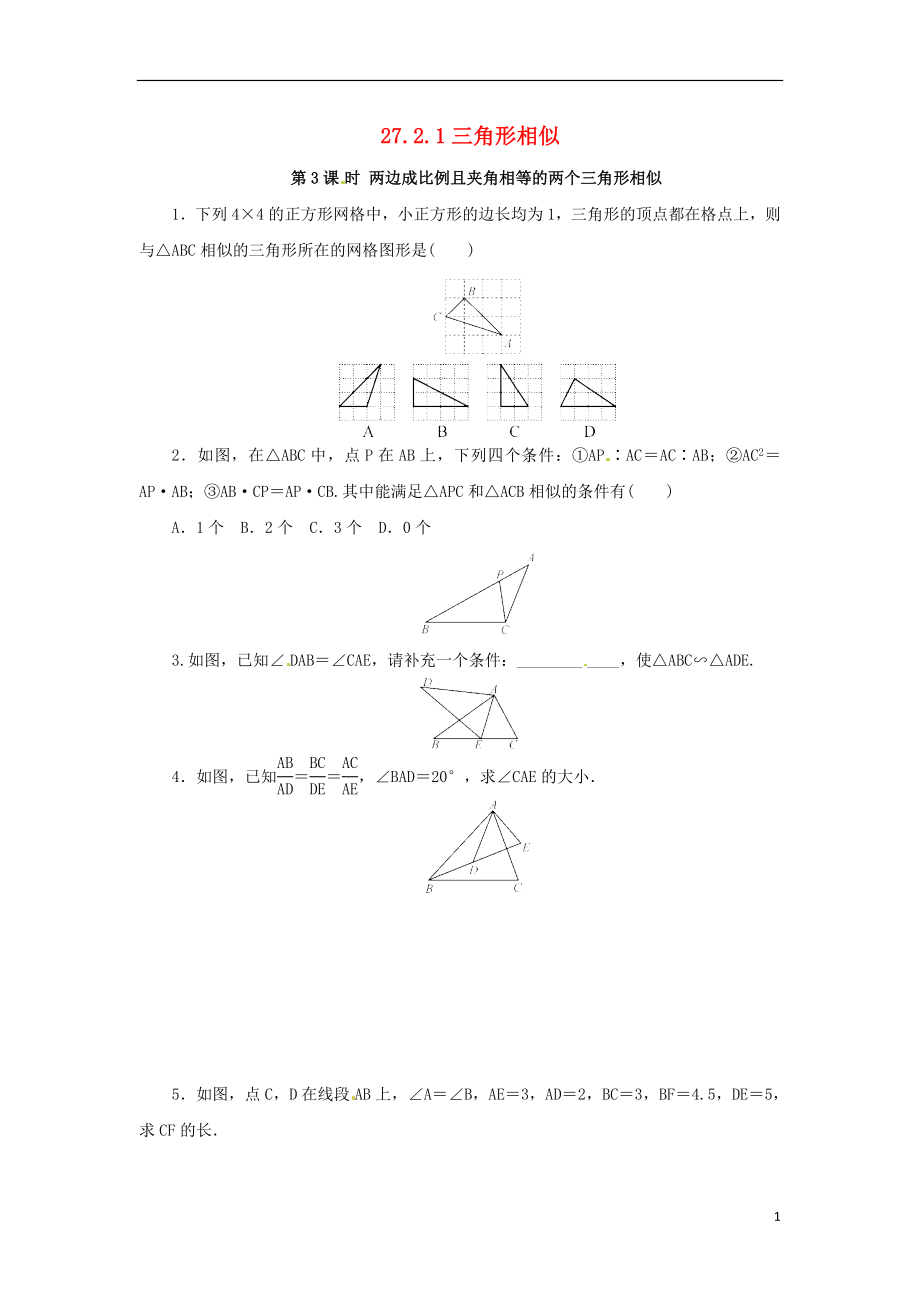
1、 27.2.1三角形相似 第3課時 兩邊成比例且夾角相等的兩個三角形相似 1．下列4×4的正方形網(wǎng)格中，小正方形的邊長均為1，三角形的頂點都在格點上，則與△ABC相似的三角形所在的網(wǎng)格圖形是(　　) 2．如圖，在△ABC中，點P在AB上，下列四個條件：①AP∶AC＝AC∶AB；②AC2＝AP·AB；③AB·CP＝AP·CB.其中能滿足△APC和△ACB相似的條件有(　　) A．1個 B．2個 C．3個 D．0個 3.如圖，已知∠DAB＝∠CAE，請補充一個條件：____________，使△ABC∽△ADE. 4．如圖，已知＝＝，∠BAD＝20°，求∠CAE

2、的大?。? 5．如圖，點C，D在線段AB上，∠A＝∠B，AE＝3，AD＝2，BC＝3，BF＝4.5，DE＝5，求CF的長． 6．已知：如圖，在△ABC中，AB＝AC，D為CB延長線上一點，E為BC延長線上一點，且滿足AB2＝DB·CE.求證：△ADB∽△EAC. 7．已知如圖，正方形ABCD中，P是BC上的點，且BP＝3PC，Q是CD的中點，求證：△ADQ∽△QCP. 8．如圖，在△ABC中，點D，E分別在邊AB，AC上，∠AED＝∠B，射線AG分別交線段DE，BC于點F，G，且＝. (

3、1)求證：△ADF∽△ACG； (2)若＝，求的值． 9．如圖，在△ABC中，AB＝AC＝1，BC＝，在AC邊上截取AD＝BC，連接BD. (1)通過計算，判斷AD2與AC·CD 的大小關(guān)系； (2)求∠ABD 的度數(shù)． 10．（2018?遵義）如圖，四邊形ABCD中，AD∥BC，∠ABC=90°，AB=5，BC=10，連接AC、BD，以BD為直徑的圓交AC于點E．若DE=3，求AD的長. 參考答案 1.B 2.B 3.＝ 4.∵＝＝， ∴△ABC∽△ADE. ∴∠BAC＝∠DA

4、E. 又∠DAC是公共角， ∴∠CAE＝∠BAD＝20°. 5.∵＝＝，＝， ∴＝. 又∠A＝∠B， ∴△AED∽△BFC， ∴＝. ∴＝. ∴CF＝. 6.證明：∵AB＝AC， ∴∠ABC＝∠ACB， ∴∠ABD＝∠ACE. ∵AB2＝DB·CE， ∴＝. 又AB＝AC， ∴＝. ∴△ADB∽△EAC. 7.證明：設(shè)正方形的邊長為4a，則AD＝CD＝BC＝4a. ∵Q是CD的中點，BP＝3PC， ∴DQ＝CQ＝2a，PC＝a. ∴＝＝. 又∵∠D＝∠C＝90°， ∴△ADQ∽△QCP.　 8.解：(1)證明：∵∠AED＝∠B，∠DAE＝∠BAC

5、， ∴∠ADF＝∠C. 又∵＝， ∴△ADF∽△ACG. (2)∵△ADF∽△ACG， ∴＝＝. ∴＝1. 9.解：(1)∵AD＝BC＝， ∴AD2＝()2＝. ∵AC＝1， ∴CD＝1－＝. ∴AD2＝AC·CD. (2)∵AD2＝AC·CD， ∴BC2＝AC·CD，即＝. 又∵∠C＝∠C， ∴△ABC∽△BDC. ∴＝. 又∵AB＝AC， ∴BD＝BC＝AD. ∴∠A＝∠ABD，∠ABC＝∠C＝∠BDC. 設(shè)∠A＝∠ABD＝x， 則∠BDC＝∠A＋∠ABD＝2x. ∴∠ABC＝∠C＝∠BDC＝2x. ∴∠A＋∠ABC＋∠C＝x＋2x＋2x＝180°. 解得x＝36°. ∴∠ABD＝36°. 10． 解：在Rt△ABC中，AB=5，BC=10， ∴AC=5 過點D作DF⊥AC于F， ∴∠AFD=∠CBA， ∵AD∥BC， ∴∠DAF=∠ACB， ∴△ADF∽△CAB， ∴， ∴， 設(shè)DF=x，則AD=x， 在Rt△ABD中，BD==， ∵∠DEF=∠DBA，∠DFE=∠DAB=90°， ∴△DEF∽△DBA， ∴， ∴， ∴x=2， ∴AD=x=2. 7