《2018年九年級(jí)數(shù)學(xué)下冊(cè) 第二十八章 銳角三角函數(shù) 28.2 解直角三角形及其應(yīng)用 28.2.2 解直角三角形的簡(jiǎn)單應(yīng)用 第1課時(shí) 解直角三角形的簡(jiǎn)單應(yīng)用隨堂檢測(cè) （新版）新人教版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2018年九年級(jí)數(shù)學(xué)下冊(cè) 第二十八章 銳角三角函數(shù) 28.2 解直角三角形及其應(yīng)用 28.2.2 解直角三角形的簡(jiǎn)單應(yīng)用 第1課時(shí) 解直角三角形的簡(jiǎn)單應(yīng)用隨堂檢測(cè) （新版）新人教版（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

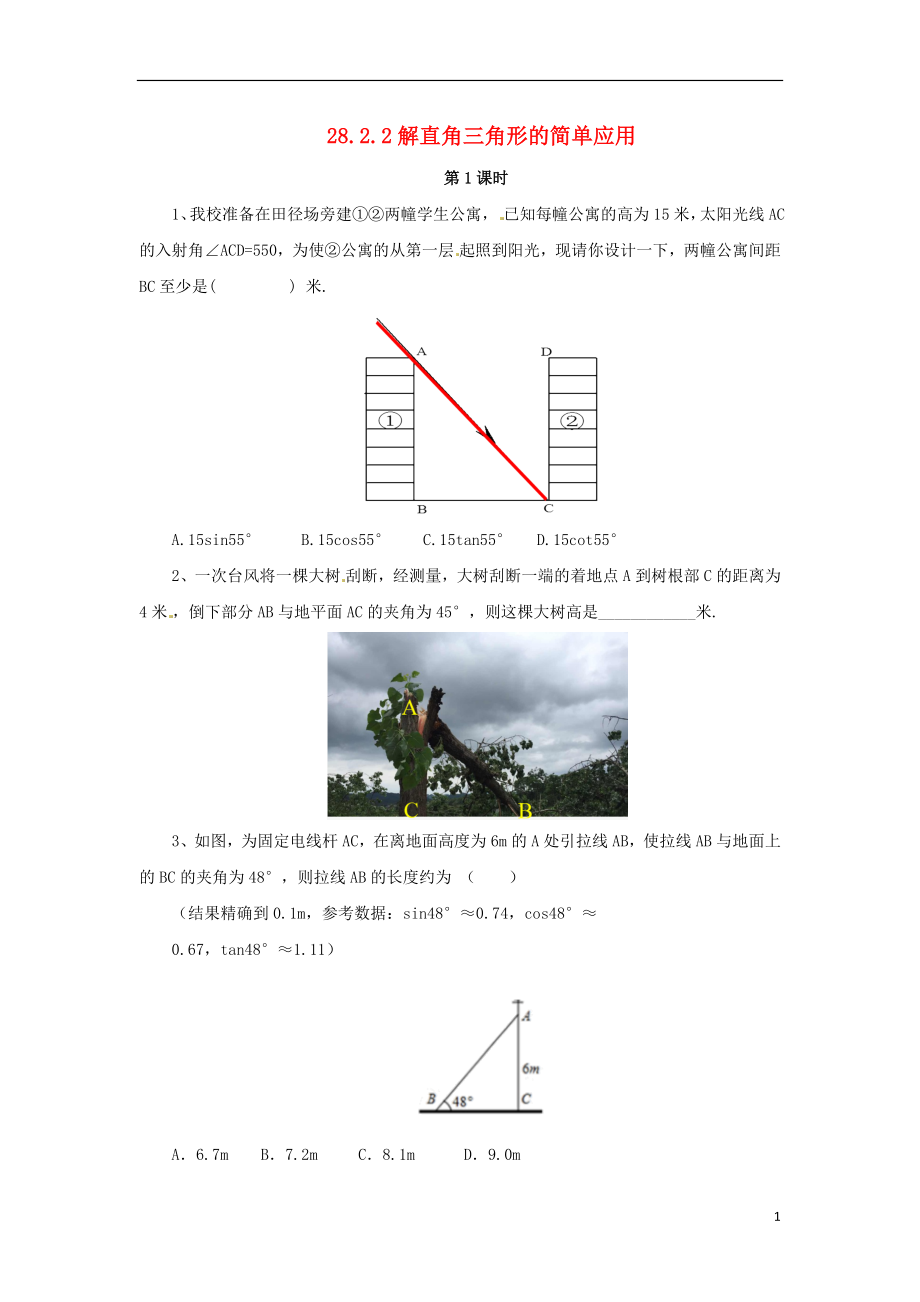
1、 28.2.2解直角三角形的簡(jiǎn)單應(yīng)用 第1課時(shí) 1、我校準(zhǔn)備在田徑場(chǎng)旁建①②兩幢學(xué)生公寓，已知每幢公寓的高為15米，太陽(yáng)光線AC的入射角∠ACD=550，為使②公寓的從第一層起照到陽(yáng)光，現(xiàn)請(qǐng)你設(shè)計(jì)一下，兩幢公寓間距BC至少是( ) 米. A.15sin55° B.15cos55° C.15tan55° D.15cot55° 2、一次臺(tái)風(fēng)將一棵大樹(shù)刮斷，經(jīng)測(cè)量，大樹(shù)刮斷一端的著地點(diǎn)A到樹(shù)根部C的距離為4米，倒下部分AB與地平面AC的夾角為45°，則這棵大樹(shù)高是____________米. 3、如圖，為固定電線桿AC，在離地面高度為6m的A處引

2、拉線AB，使拉線AB與地面上的BC的夾角為48°，則拉線AB的長(zhǎng)度約為 （　?。? （結(jié)果精確到0.1m，參考數(shù)據(jù)：sin48°≈0.74，cos48°≈ 0.67，tan48°≈1.11） A．6.7m B．7.2m C．8.1m D．9.0m 4、數(shù)學(xué)課外興趣小組的同學(xué)們要測(cè)量被池塘相隔的兩棵樹(shù)A、B的距離，他們?cè)O(shè)計(jì)了如圖所示的測(cè)量方案：從樹(shù)A沿著垂直于AB的方向走到E，再?gòu)腅沿著垂直于AE的方向走到F，C為AE上一點(diǎn)，其中3位同學(xué)分別測(cè)得三組數(shù)據(jù)：①AC，∠ACB；②EF、DE、AD；③CD，∠ACB，∠ADB．其中能根據(jù)所測(cè)數(shù)據(jù)求得A、B兩樹(shù)距離的有（

3、　?。? A．0組 B.1組 C．2組 D.3組 5、某居民小區(qū)有一朝向?yàn)檎戏较虻木用駱?該居民樓的一樓是高6米的小區(qū)超市,超市以上是居民住房.在該樓的前面15米處要蓋一棟高20米的新樓.當(dāng)冬季正午的陽(yáng)光與水平線的夾角為30°時(shí).問(wèn)：超市以上的居民住房采光是否有影響,為什么？ （1）小華去實(shí)驗(yàn)樓做實(shí)驗(yàn), 兩幢實(shí)驗(yàn)樓的高度AB=CD=20m, 兩樓間的距離BC=15m，已知太陽(yáng)光與水平線的夾角為30°，求南樓的影子在北樓上有多高？ （2）小華想:若設(shè)計(jì)時(shí)要求北樓的采光,不受南樓的影響,請(qǐng)問(wèn)樓間距 BC長(zhǎng)至少應(yīng)為多少米? 參考答案 1、C 2、 3、C 4、D 5、解：（1）解：過(guò)點(diǎn)E作EF∥BC， ∴∠AFE=90°，F(xiàn)E=BC=15m. 即南樓的影子在北樓上的高度為 (2)BC至少為 3