《2022年高考數(shù)學(xué)一輪復(fù)習(xí) 3.3 冪函數(shù)教案 新課標(biāo)》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年高考數(shù)學(xué)一輪復(fù)習(xí) 3.3 冪函數(shù)教案 新課標(biāo)（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

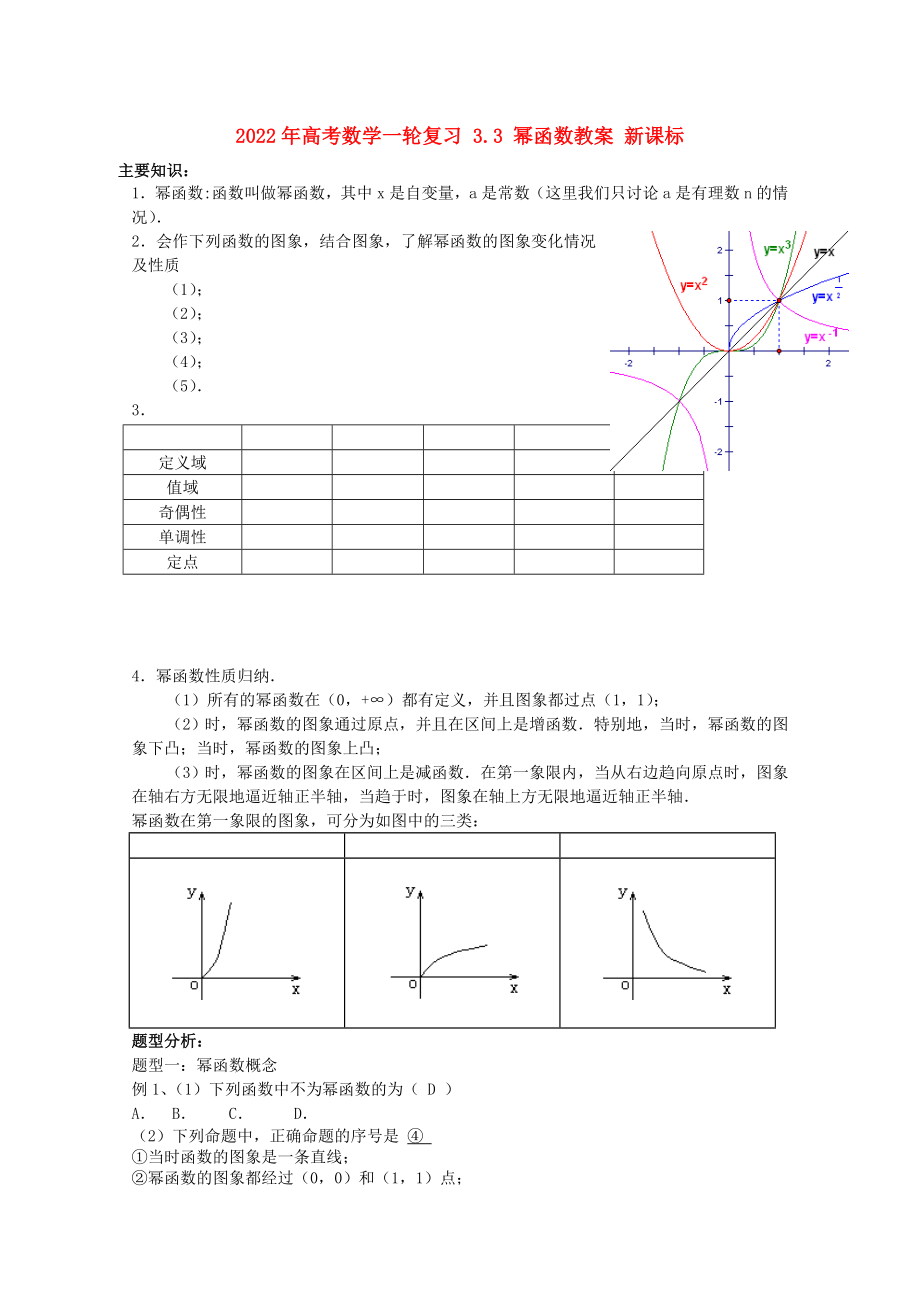
1、2022年高考數(shù)學(xué)一輪復(fù)習(xí) 3.3 冪函數(shù)教案 新課標(biāo) 主要知識(shí)： 1．冪函數(shù):函數(shù)叫做冪函數(shù)，其中x是自變量，a是常數(shù)（這里我們只討論a是有理數(shù)n的情況）． 2．會(huì)作下列函數(shù)的圖象，結(jié)合圖象，了解冪函數(shù)的圖象變化情況及性質(zhì) （1）； （2）； （3）； （4）； （5）． 3． 定義域 值域 奇偶性 單調(diào)性 定點(diǎn) 4．冪函數(shù)性質(zhì)歸納． （1）所有的冪函數(shù)在（0，+∞）都有定義，并且圖象都過點(diǎn)（1，1）；

2、 （2）時(shí)，冪函數(shù)的圖象通過原點(diǎn)，并且在區(qū)間上是增函數(shù)．特別地，當(dāng)時(shí)，冪函數(shù)的圖象下凸；當(dāng)時(shí)，冪函數(shù)的圖象上凸； （3）時(shí)，冪函數(shù)的圖象在區(qū)間上是減函數(shù)．在第一象限內(nèi)，當(dāng)從右邊趨向原點(diǎn)時(shí)，圖象在軸右方無限地逼近軸正半軸，當(dāng)趨于時(shí)，圖象在軸上方無限地逼近軸正半軸． 冪函數(shù)在第一象限的圖象，可分為如圖中的三類： 題型分析： 題型一：冪函數(shù)概念 例1、（1）下列函數(shù)中不為冪函數(shù)的為（ D ） A． B． C． D． （2）下列命題中，正確命題的序號(hào)是 ④ ①當(dāng)時(shí)函數(shù)的圖象是一條直線； ②冪函數(shù)的圖象都經(jīng)過（0，0）和

3、（1，1）點(diǎn)； ③若冪函數(shù)是奇函數(shù)，則是定義域上的增函數(shù)； ④冪函數(shù)的圖象不可能出現(xiàn)在第四象限． 例2（1）函數(shù)的定義域是（B　?。? A．{x|x≠0或x≠2}B．（－∞，0）（2，＋∞）C．（－∞，0）［2，＋∞?。〥．（0，2） （2）已知冪函數(shù)的圖象不過原點(diǎn)，則m的值為_________。3 題型二：冪函數(shù)圖象性質(zhì) 例3（1）當(dāng)x∈（1，+∞）時(shí)，函數(shù)的圖象恒在y=x的下方，則a的取值范圍是_________。a＜1 （2）右圖為冪函數(shù)在第一象限的圖象，則按由小到大的順序排列為 例4冪函數(shù)，當(dāng)取不同的正數(shù)時(shí)，在區(qū)間上它們的圖象是一族美麗的曲線（如圖），設(shè)點(diǎn)，連結(jié)，線段恰

4、好被其中的兩個(gè)冪函數(shù)的圖象三等分，即有。那么 。 題型三：比較大小 例5．（1）若，比較的大小；（2）若，比較的大?。? 解：（1）當(dāng)時(shí)，冪函數(shù)在上單調(diào)減，∵，∴． （2）當(dāng)時(shí)，，指數(shù)函數(shù)在上單調(diào)減， ∵，∴，∴ ， ∴ 題型四：冪函數(shù)的綜合應(yīng)用 例6．已知冪函數(shù)的圖象與軸、軸都無交點(diǎn)，且關(guān)于軸對(duì)稱，試確定的解析式． 解：由數(shù)，解得：． 當(dāng)和3時(shí)，；當(dāng)時(shí)，． 備用： 已知函數(shù) （1）求函數(shù)的定義域、值域； （2）判斷函數(shù)的奇偶性； （3）求函數(shù)的單調(diào)區(qū)間. 解：這是復(fù)合函數(shù)問題，利用換元法令t＝15－2x－x2，則y＝， （1）由15－2x－x2≥0得函數(shù)

5、的定義域?yàn)椋郏?，3］， ∴t＝16－（x－1）2［0，16］．∴函數(shù)的值域?yàn)椋?，2］． （2）∵函數(shù)的定義域?yàn)椋郏?，3］且關(guān)于原點(diǎn)不對(duì)稱，∴函數(shù)既不是奇函數(shù)也不是偶函數(shù)． （3）∵函數(shù)的定義域?yàn)椋郏?，3］，對(duì)稱軸為x＝1， ∴x［－5，1］時(shí)，t隨x的增大而增大；x（1，3）時(shí)，t隨x的增大而減?。? 又∵函數(shù)y＝在t［0，16］時(shí)，y隨t的增大而增大， ∴函數(shù)y＝的單調(diào)增區(qū)間為［－5，1］，單調(diào)減區(qū)間為（1，3）． 作業(yè)：《走向高考》 作業(yè):1.比較下列各數(shù)的大小 2． 已知，求的取值范圍. 答案： 3.已知函數(shù) 為偶函數(shù)，且f(3)