《（新課標）2020版高考數(shù)學二輪復習 專題五 解析幾何 高考解答題的審題與答題示范（五）解析幾何類解答題學案 理 新人教A版》由會員分享，可在線閱讀，更多相關《（新課標）2020版高考數(shù)學二輪復習 專題五 解析幾何 高考解答題的審題與答題示范（五）解析幾何類解答題學案 理 新人教A版（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

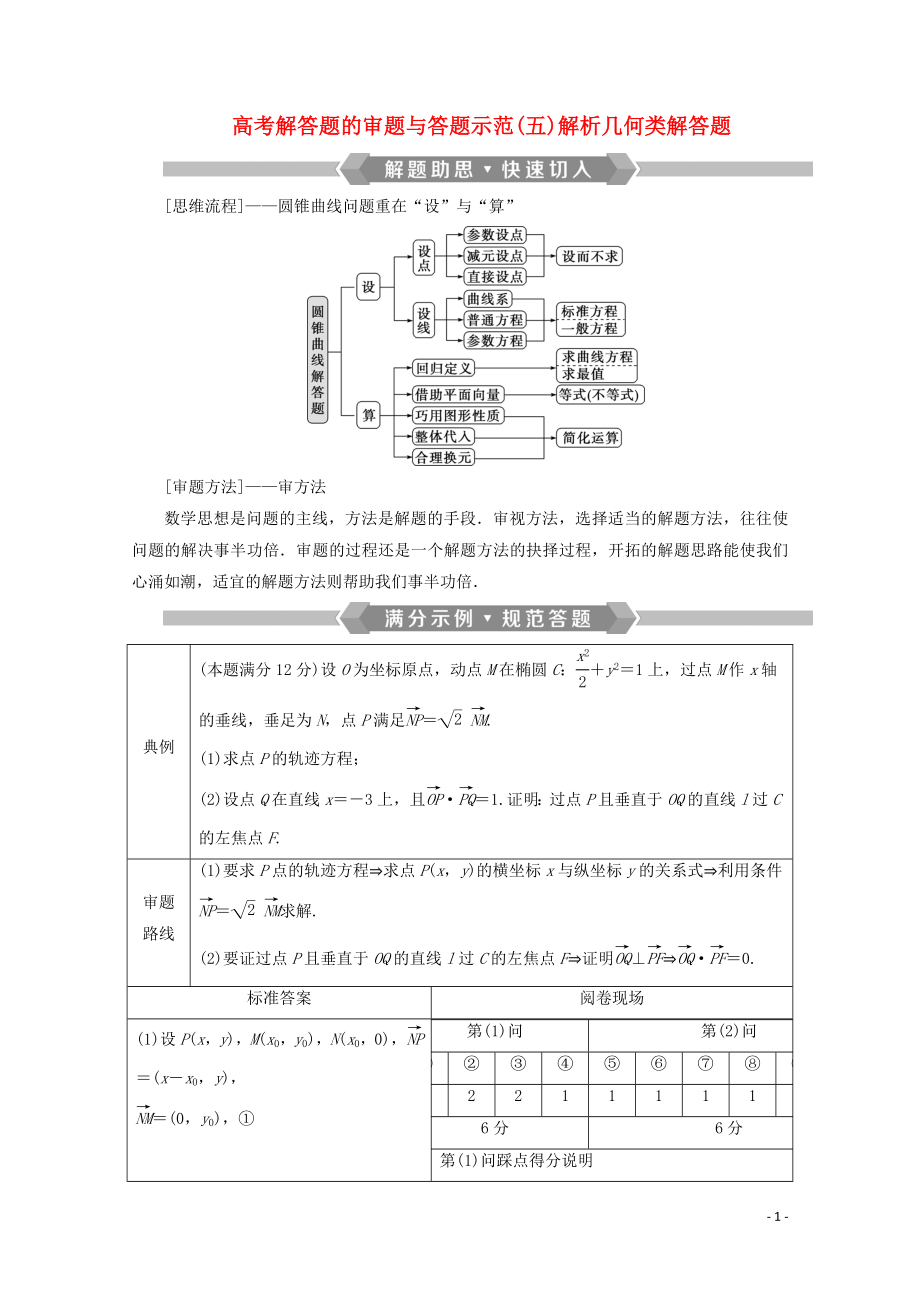
1、高考解答題的審題與答題示范(五)解析幾何類解答題 [思維流程]——圓錐曲線問題重在“設”與“算” [審題方法]——審方法 數(shù)學思想是問題的主線，方法是解題的手段．審視方法，選擇適當?shù)慕忸}方法，往往使問題的解決事半功倍．審題的過程還是一個解題方法的抉擇過程，開拓的解題思路能使我們心涌如潮，適宜的解題方法則幫助我們事半功倍． 典例 (本題滿分12分)設O為坐標原點，動點M在橢圓C：＋y2＝1上，過點M作x軸的垂線，垂足為N，點P滿足＝ . (1)求點P的軌跡方程； (2)設點Q在直線x＝－3上，且·＝1.證明：過點P且垂直于OQ的直線l過C的左焦點F. 審題 路線

2、(1)要求P點的軌跡方程?求點P(x，y)的橫坐標x與縱坐標y的關系式?利用條件＝ 求解. (2)要證過點P且垂直于OQ的直線l過C的左焦點F?證明⊥?·＝0. 標準答案 閱卷現(xiàn)場 (1)設P(x，y)，M(x0，y0)，N(x0，0)，＝(x－x0，y)， ＝(0，y0)，① 由＝ ， 得x0＝x，y0＝y(tǒng)，② 因為M(x0，y0)在C上， 所以＋＝1，③ 因此點P的軌跡方程為x2＋y2＝2.④ (2)證明：由題意知F(－1，0)， 設Q(－3，t)，P(m，n)設而不求， 則＝(－3，t)，＝(－1－m，－n)，⑤ ·＝3＋3m－tn，⑥ ＝(m，n)，＝(－

3、3－m，t－n)，⑦ 由·＝1得－3m－m2＋tn－n2＝1，⑧ 又由(1)知m2＋n2＝2，故3＋3m－tn＝0. 所以·＝0，即⊥，⑨ 又過點P存在唯一直線垂直于OQ，所以過點P且垂直于OQ的直線l過C的左焦點F.⑩ 第(1)問 第(2)問 得 分 點 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ 1 2 2 1 1 1 1 1 1 1 6分 6分 第(1)問踩點得分說明 ①設出點P、M、N的坐標，并求出和的坐標得1分； ②由＝ ，正確求出x0＝x，y0＝y(tǒng)得2分； ③代入法求出＋＝1得2分； ④化簡成x2＋y2＝2得1分. 第(2)問踩點得分說明 ⑤求出和的坐標得1分； ⑥正確求出·的值得1分； ⑦正確求出和的坐標得1分； ⑧由·＝1得出－3m－m2＋tn－n2＝1得1分； ⑨得出⊥得1分； ⑩寫出結論得1分. - 3 -