《2022年高考數(shù)學(xué)二輪復(fù)習(xí) 專題五 立體幾何 專題突破練17 5.1~5.3組合練 文》由會員分享，可在線閱讀，更多相關(guān)《2022年高考數(shù)學(xué)二輪復(fù)習(xí) 專題五 立體幾何 專題突破練17 5.1~5.3組合練 文（6頁珍藏版）》請在裝配圖網(wǎng)上搜索。

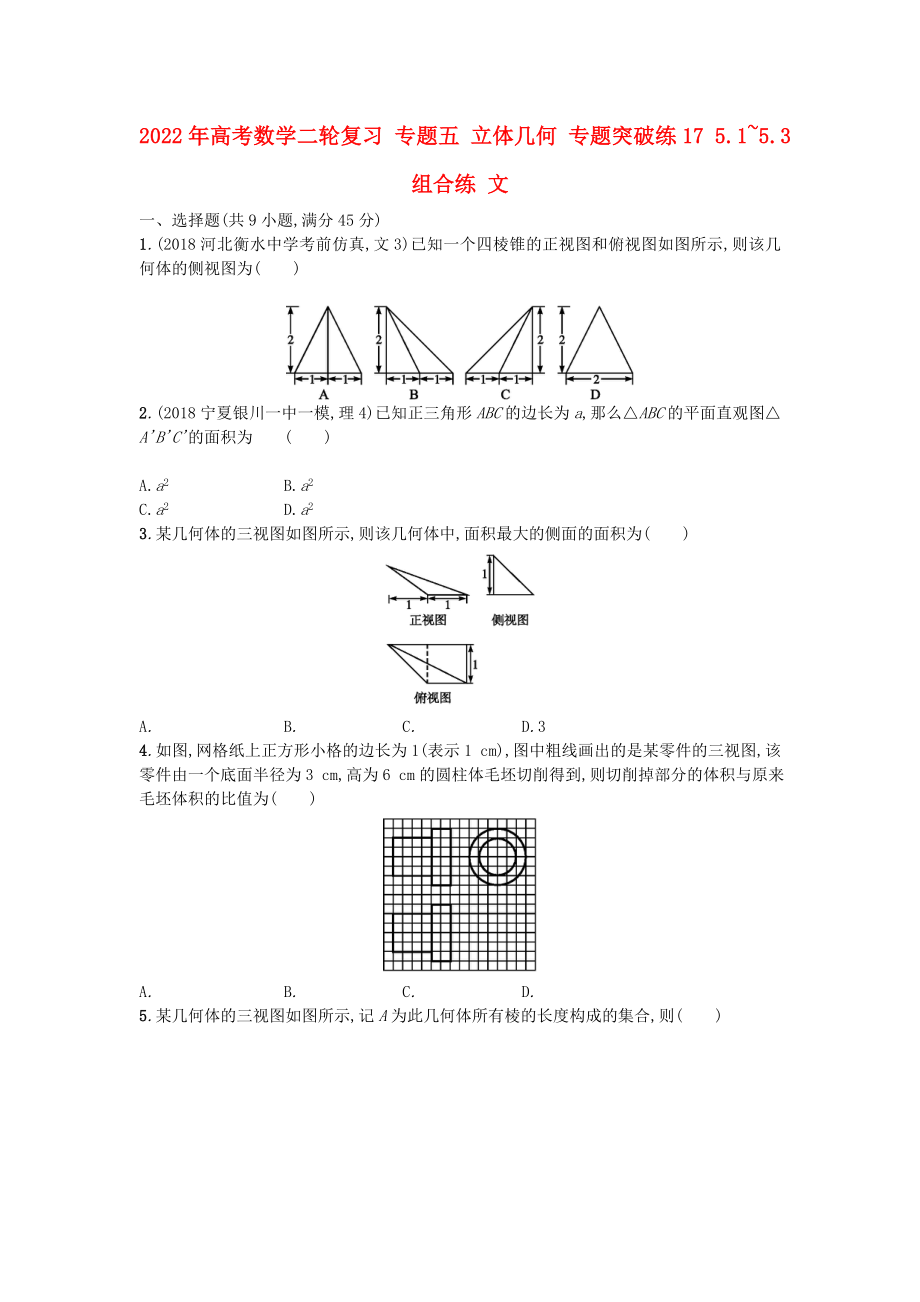
1、2022年高考數(shù)學(xué)二輪復(fù)習(xí) 專題五 立體幾何 專題突破練17 5.1~5.3組合練 文 一、選擇題(共9小題,滿分45分) 1.(2018河北衡水中學(xué)考前仿真,文3)已知一個四棱錐的正視圖和俯視圖如圖所示,則該幾何體的側(cè)視圖為(　　) 2.(2018寧夏銀川一中一模,理4)已知正三角形ABC的邊長為a,那么△ABC的平面直觀圖△A'B'C'的面積為 (　　) 　 　　　　　　　　　　　　　　　 A.a2 B.a2 C.a2 D.a2 3.某幾何體的三視圖如圖所示,則該幾何體中,面積最大的側(cè)面的面積為(　　) A. B. C. D.3 4.如圖,網(wǎng)格紙上正方形小格的

2、邊長為1(表示1 cm),圖中粗線畫出的是某零件的三視圖,該零件由一個底面半徑為3 cm,高為6 cm的圓柱體毛坯切削得到,則切削掉部分的體積與原來毛坯體積的比值為(　　) A. B. C. D. 5.某幾何體的三視圖如圖所示,記A為此幾何體所有棱的長度構(gòu)成的集合,則(　　) A.3∈A B.5∈A C.2∈A D.4∈A 6.(2018河北唐山三模,理7)某三棱錐的三視圖如圖所示,則其體積為(　　) A.4 B.8 C. D. 7.已知正三棱柱ABC-A1B1C1的底面邊長為2,側(cè)棱長為,D為BC的中點,則三棱錐A-B1DC1的體積為(　　) A.3 B. C.1

3、 D. 8.(2018河南濮陽一模,理7)已知三棱錐A-BCD中,△ABD與△BCD是邊長為2的等邊三角形且二面角A-BD-C為直二面角,則三棱錐A-BCD的外接球的表面積為(　　) A. B.5π C.6π D. 9.(2018山西呂梁一模,文12)已知點A,B,C,D在同一個球的球面上,AB=BC=,AC=2,若四面體ABCD的體積為,球心O恰好在棱DA上,則這個球的表面積為 (　　) A. B.4π C.8π D.16π 二、填空題(共3小題,滿分15分) 10.(2018江蘇卷,10)如圖所示,正方體的棱長為2,以其所有面的中心為頂點的多面體的體積為　　　　　.? 1

4、1.(2018天津卷,文11)如圖,已知正方體ABCD-A1B1C1D1的棱長為1,則四棱錐A1-BB1D1D的體積為　　　　　　.? 12.已知三棱錐A-BCD,AB=AC=BC=2,BD=CD=,點E是BC的中點,點A在平面BCD上的射影恰好為DE的中點F,則該三棱錐外接球的表面積為　　　　　.? 三、解答題(共3個題,分別滿分為13分,13分,14分) 13.(2018江蘇南京、鹽城一模,15)如圖所示,在直三棱柱ABC-A1B1C1中,CA=CB,點M,N分別是AB,A1B1的中點. (1)求證:BN∥平面A1MC; (2)若A1M⊥AB1,求證:AB1⊥A1C.

5、 14.(2018河南六市聯(lián)考一,文19)如圖,已知四棱錐S-ABCD中,底面ABCD是邊長為2的菱形,∠BAD=60°,SA=SD=,SB=,點E是棱AD的中點,點F在棱SC上,且=λ,SA∥平面BEF. (1)求實數(shù)λ的值; (2)求三棱錐F-EBC的體積. 15.如圖1,在邊長為2的正方形ABCD中,點E是AB的中點,點F是BC的中點.將△AED,△DCF分別沿DE,DF折起,使A,C兩點重合于點A',連接EF,A'B,如圖2. (1)求異面直線A'D與EF所成角的大小; (2)求三棱錐D-A'EF的體積.

6、 參考答案 專題突破練17　5.1~5.3組合練 1.A　解析 四棱錐的正視圖和俯視圖可知幾何體的直觀圖如圖所示,其側(cè)視圖為選項A. 2.D　解析 如圖①②所示的平面圖形和直觀圖.由②可知,A'B'=AB=a,O'C'=OC=a, 在圖②中作C'D'⊥A'B'于D', 則C'D'=O'C'=a. ∴S△A'B'C'=A'B'·C'D'=×a×a=a2. 3.B　解析 由三視圖可知,幾何體的直觀圖如圖所示,平面AED⊥平面BCDE,四棱錐A-BCDE的高為1,四邊形BCDE是邊長為1的正方形,則S△AED=×1×1

7、=,S△ABC=S△ABE=×1×,S△ACD=×1×,故選B. 4.C　解析 由零件的三視圖可知,該幾何體為兩個圓柱組合而成,如圖所示. 切削掉部分的體積V1=π×32×6-π×22×4-π×32×2=20π(cm3), 原來毛坯體積V2=π×32×6=54π(cm3).故所求比值為. 5.D　解析 根據(jù)三視圖可知幾何體是一個三棱柱截去一個三棱錐,如圖所示,四邊形ABCD是一個邊長為4的正方形, 且AF⊥面ABCD,DE∥AF,DE=4,AF=2, ∴AF⊥AB,DE⊥DC,DE⊥BD, ∴EC==4,EF=FB==2,BE==4. ∵A為此幾何體所有棱的長度

8、構(gòu)成的集合,∴A={2,4,4,4,2}. 6.C　解析 由三棱錐的三視圖得其直觀圖如下:幾何體為底面是等腰直角三角形的三棱錐A-BCD,BC=CD=2,三棱錐的高為2,所以三棱錐的體積為V=×2×2×2=. 7.C　解析 ∵D是等邊三角形ABC的邊BC的中點,∴AD⊥BC. 又ABC-A1B1C1為正三棱柱, ∴AD⊥平面BB1C1C. ∵四邊形BB1C1C為矩形, ∴×2×.又AD=2×, ∴·AD==1.故選C. 8.D　解析 如圖所示. △ABD與△BCD是邊長為2的等邊三角形,且二面角A-BD-C為直二面角, 設(shè)F,E分別為△ABD和△BCD的中心,則球心

9、O為△ABD和△BCD的過中心的垂線的交點,所以O(shè)F=OE=FG=×2=. ED=×2=, 則球半徑r=,則S=4π×. 9.D　解析 如圖所示,設(shè)AC的中點為M,由已知得AB⊥BC,所以底面三角形ABC外接圓的圓心為M,所以O(shè)M⊥平面ABC,又OM∥DC,所以DC⊥平面ABC,由四面體的體積為,得DC=2. 所以DA=4,球的半徑為2,由球的表面積公式得球的表面積為16π.選D. 10.　解析 由題圖可知,該多面體為兩個全等的正四棱錐的組合體,且正四棱錐的高為1,底面正方形的邊長為,所以該多面體的體積為2××()2×1=. 11.　解析 ∵正方體ABCD-A1B1C1D1的棱

10、長為1, ∴=V正方體-=1-×1×1×1-×1×1×1=. 12.　解析 由題意,得△BCD為等腰直角三角形,E是外接圓的圓心. ∵點A在平面BCD上的射影恰好為DE的中點F,∴BF=, ∴AF=. 設(shè)球心O到平面BCD的距離為h,則1+h2=,解得h=,r=,故該三棱錐外接球的表面積為4π×. 13.證明 (1)因為ABC-A1B1C1是直三棱柱, 所以AB∥A1B1,且AB=A1B1, 又點M,N分別是AB,A1B1的中點,所以MB=A1N,且MB∥A1N. 所以四邊形A1NBM是平行四邊形,從而A1M∥BN. 又BN?平面A1MC,A1M?平面A1MC,所以BN

11、∥面A1MC. (2)因為ABC-A1B1C1是直三棱柱, 所以AA1⊥底面ABC,而AA1?側(cè)面ABB1A1, 所以側(cè)面ABB1A1⊥底面ABC. 又CA=CB,且M是AB的中點,所以CM⊥AB. 則由側(cè)面ABB1A1⊥底面ABC,側(cè)面ABB1A1∩底面ABC=AB,CM⊥AB,且CM?底面ABC,得CM⊥側(cè)面ABB1A1. 又AB1?側(cè)面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M,MC?平面A1MC,且A1M∩MC=M, 所以AB1⊥平面A1MC. 又A1C?平面A1MC,所以AB1⊥A1C. 14.解 (1)連接AC,設(shè)AC∩BE=G,則平面SAC∩平面E

12、FB=FG, ∵△GEA∽△GBC,∴.∴. ∴SF=SC,∴λ=. (2)連接SE,∵SA=SD=, ∴SE⊥AD,SE=2. ∵AB=AD=2,∠BAD=60°, ∴BE=. ∵SE2+BE2=SB2,∴SE⊥BE. ∴SE⊥平面ABCD. 所以VF-BCE=VS-EBC=VS-ABCD=×2×2sin 60°×2=. 15.解 (1)在正方形ABCD中,∵AD⊥AE,CD⊥CF,∴A'D⊥A'E,A'D⊥A'F. ∵A'E∩A'F=A',A'E,A'F?平面A'EF,∴A'D⊥平面A'EF. 而EF?平面A'EF,∴A'D⊥EF, ∴異面直線A'D與EF所成角的大小為90°. (2)∵正方形ABCD的邊長為2,點E是AB的中點,點F是BC的中點,∴在Rt△BEF中,BE=BF=1,得EF=,而A'E=A'F=1, ∴A'E2+A'F2=EF2,∴A'E⊥A'F, ∴S△A'EF=×1×1=. 由(1)得A'D⊥平面A'EF,且A'D=2,∴VD-A'EF=S△A'EF·A'D=×2=.