對高三數(shù)學首輪復習解題教學的建議尤榮勇高三數(shù)學首輪復習成功與否直接關系到第二輪復習及后繼復習的順利進行，而解題教學是首輪復習中的一個重要環(huán)節(jié)，如何針對首輪復習的特點，輕松高效的做好解題教學，是我們締畢業(yè)班數(shù)學老師所追求的目標，筆者根據(jù)多年的高三復習實踐經(jīng)驗，談談自己的體會，供同仁們在教學中參考。1 注重解題規(guī)范性、示范性、提高學生解題準確率ANDCMB規(guī)范的解題能夠使學生養(yǎng)成良好的學習習慣，拉高思維水平，規(guī)范的解題主要包括審題規(guī)范，語言表達規(guī)范、答案規(guī)范。審題是對題目進行分析、綜合、尋求解題思路和方法的過程，所以審題規(guī)范是正確解題的先決條件，而語言表達規(guī)范和答案規(guī)范是檢驗學生對知識的認識程度。大家都知道，高考試卷中主觀題的評分標準都是分步給分的。一般來說，老師地高一、高二新授課教學時，能規(guī)范示范，學生也能規(guī)范答題，但到了高三，老師往往更注重大容量的題海戰(zhàn)術，學生也疲于奔命，結果是老師講了不少題，學生做了不少題，但最終學生的能力幾乎沒有多大提高 ，在高考中也就沒有多大的競爭力。如果我們從平時嚴格要求學生，能在每節(jié)課盡量做到示范一道題的解題過程，這對提高學生解題正確率大有裨益。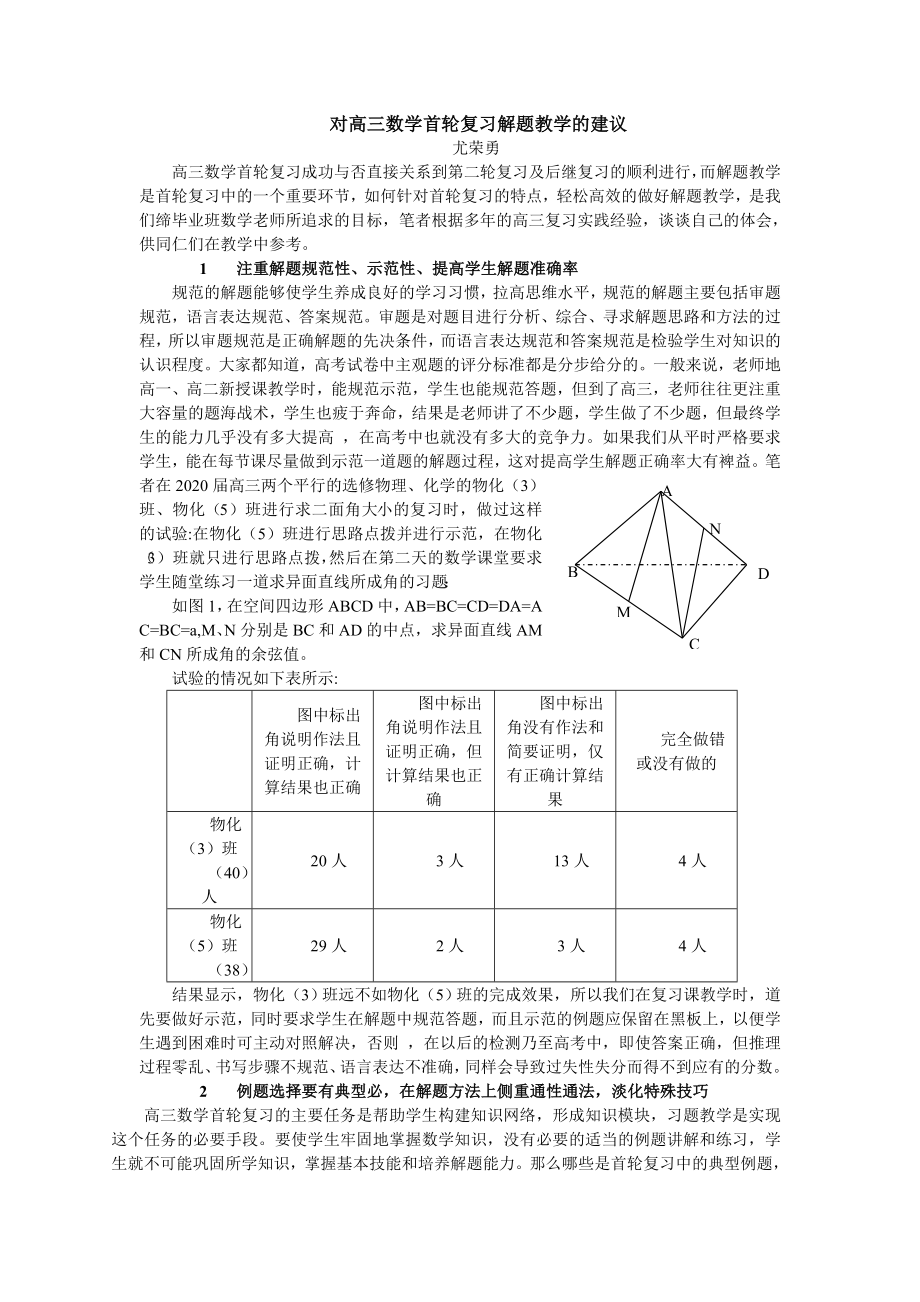筆者在2020屆高三兩個平行的選修物理、化學的物化（3）班、物化（5）班進行求二面角大小的復習時，做過這樣的試驗:在物化（5）班進行思路點撥并進行示范，在物化（3）班就只進行思路點撥，然后在第二天的數(shù)學課堂要求學生隨堂練習一道求異面直線所成角的習題：如圖1，在空間四邊形ABCD中，AB=BC=CD=DA=A C=BC=a,M、N分別是BC和AD的中點，求異面直線AM和CN所成角的余弦值。試驗的情況如下表所示:圖中標出角說明作法且證明正確，計算結果也正確圖中標出角說明作法且證明正確，但計算結果也正確圖中標出角沒有作法和簡要證明，僅有正確計算結果完全做錯或沒有做的物化（3）班（40）人20人3人13人4人物化（5）班（38）29人2人3人4人結果顯示，物化（3）班遠不如物化（5）班的完成效果，所以我們在復習課教學時，道先要做好示范，同時要求學生在解題中規(guī)范答題，而且示范的例題應保留在黑板上，以便學生遇到困難時可主動對照解決，否則 ，在以后的檢測乃至高考中，即使答案正確，但推理過程零亂、書寫步驟不規(guī)范、語言表達不準確，同樣會導致過失性失分而得不到應有的分數(shù)。2 例題選擇要有典型必，在解題方法上側重通性通法，淡化特殊技巧高三數(shù)學首輪復習的主要任務是幫助學生構建知識網(wǎng)絡，形成知識模塊，習題教學是實現(xiàn)這個任務的必要手段。要使學生牢固地掌握數(shù)學知識，沒有必要的適當?shù)睦}講解和練習，學生就不可能鞏固所學知識，掌握基本技能和培養(yǎng)解題能力。那么哪些是首輪復習中的典型例題，筆者的理解是，它不是那些偏題、難題、怪題，而是在問題中能融入相關知識點、富有啟發(fā)性，通過該問題的解決，有促使學生理解知識，掌握方法，獲取新見解的題，何等典型性的例題即具有代表性，研究它的典型意義，可以“以點代面”使學生舉一反三、觸類旁通。例如在解析幾何中用代入法求動點軌跡問題。我們不妨選擇這樣的例題;QyOPA(2,0)x如圖2，設A的坐標為（2，0），Q為圓x2+y2=1上任一點，OP是AOQ中AOQ的平分線，求P點的軌跡。 圖2 解決問題可以用通性通法-“代入法”來解決，同時從這個問題中可以抽象用該發(fā)求動點軌跡的一般模型和方法：設點P得點出Q代入已知曲線方程。 結合首輪復習的特點，包含知識點多，但思維跨度、運算量特別大的題我們要少選，甚至不選。因為學生在首輪復習中還不具備那樣的能力，所以選擇這樣的題不僅不能殺使學生掌握解題技巧，提高思維能力，相反，容易使學生對數(shù)學產(chǎn)生畏懼心理，逐漸對數(shù)學失去興趣，拔苗助長，得不償失！為此教師必須對例題和練習題精心設計和選擇。那么，這些典型例題的資源來自哪里？可以是以前教學中積累的，也可以是從抱刊雜志、網(wǎng)絡等渠道獲取的，當然切不可忽視課本中的一些例題和習題，因為課本中的例題和習題都是經(jīng)過專家、學者反復推敲而選定的，它具有一定的方向性和輻射性，無論是全國試卷還是各省自主命題的試卷許多考題都是由課本習題演變、改裝而成的。如果學生對這些課本上的知識真正搞懂了，那么，那些考題也就迎刃而解了。 3通過一題多解、一題多變，發(fā)揮例題的增值功能ABCD在高三首輪復習中，如何使例題在有限的時間內(nèi)發(fā)揮出較大的功能？一般教學經(jīng)驗豐富的教師，可使例題縱橫延伸主要是指對例題的一題多解的探討，縱向延伸主要是指改變例題的條件和結論，采取有層次的一題多變的變式教學，例如人教版第二冊（下B）的習題9.8的第4題：如圖3，已知正方體ABCD-的棱長為1，求直線DA與AC的距離。教師可以引導學生從不同的入口，挖掘不同的解法。解法1：AC平面,點A到平面的距離h就等于異面直線AC與D的距離，從而轉化為點而距。解法2：解法 3：不妨在AC上任取一點H，過H作GHAD交AD于點G，則GH平面AD,在上再任取一點F，轉化為異面直線 上任意兩點距離的最小值。解法4:以D為坐標原點建立空間直角坐標系，則D(0,0,0),A(1,0,0),C(0,1,0),(0,0,1),(1,0,1),設MN的一個方向向量為,利用得即為所求的距離，在教學中，教師應發(fā)掘問題的多解因素，結合學生的實際情況，鼓勵學生以問題為出發(fā)點，不囿于單一的解題思路和方法，引導學生在解法上求異，盡可能尋求較多的解題思路、方法。而教學中通過一題多變的教學手段，能使學生深刻吃透知識 的外延與內(nèi)涵，讓他們掌握其內(nèi)涵發(fā)展與免戰(zhàn)牌變換，使其對知識能融會貫通，從而培養(yǎng)學生思維的深刻性，提高他們分析問題、解決問題的能力，例如在復習集合的運算時，筆者采用了如下手段：已知集合A=xy=x2,xR,B=xx2=1,求AB.學生完成這道題后，做了如下變式題：變題1：A=y y=x2,xR,B=xx2=1,求AB。變題2：A=(x,y)y=x2,xR，B=xx2=1,求AB.變題3：A=(x,y)y=x2,xR，B=(x,y)x2=1,求AB.變題4：A=x+yy=x2,xR，B=xx2=1,求AB.通過這一組變題，層層推進，使學生對“元素”、“交集”的認識和理解呈螺旋式上升，從而對知識的理解 更加深刻，培養(yǎng)了學生思維的深刻性。一題多解、一題多變不僅增強了例題的使用價值，同時培養(yǎng)了學生的發(fā)散思維能力，挖掘出學生的創(chuàng)新潛力，形成探究意識，從而達到以一勝多的功效。4.錯解剖析、正本清源，改善學生的思維品質(zhì)在首輪復習教學中，我們發(fā)現(xiàn) ，有一些錯誤是學生的共性。如何避免他們在以后的二輪復習是中不出錯或是少出錯，是值得我們研究的問題，如果一味地把正確的解法 拋給他們，盡管暫時學生會理解它，查時間一長，往往又所剩無幾。筆者通過多年的實踐，感覺到如果把學生經(jīng)常出現(xiàn) 的錯誤，適時作以展示 ，讓他們自己首先來糾錯，這樣處理印象會比較深刻。例如解含有參數(shù)的二次函數(shù)、二次不等式的有關問題時，學生經(jīng)常會漏考慮二次項系數(shù)；求等比數(shù)列前n項和時，學生會漏考慮公比為1的情況研究函數(shù)奇偶性時，學生會漏考慮函數(shù)的定義域關于原點對稱等等；筆者就把學生作業(yè)中或測驗中出現(xiàn)的這些原汁原味的錯誤（有些甚至是前幾屆學生出現(xiàn)的錯誤）在課堂上展示，通過這種錯解剖析、以錯糾錯來正本清源，易于學生對知識深刻理解、掌握，改善思維品質(zhì)。反之，如果我們總是把正確的答案直接奉送給學生，則不能暴露問題的矛盾，也達不到預期的效果。5.指導學生題后反思，總結解題規(guī)律，提升探究能力認真并正確解題，有助于理解知識，發(fā)現(xiàn)問題，發(fā)展能力，但是解完題后并不意味著學習結束。解題以后教師要引導 學生進行反思 ，進一步理解 、總結 ，多問幾個為什么，把每道題的知識點，題型 結構、類型，條件與結論的關系等理解透徹，題后反思 ，便于總結解題規(guī)律，優(yōu)化解題方法從而能趕到擺脫題海戰(zhàn)術、以少勝多、事半功倍的錁。題后反思 還有利于積累經(jīng)驗，鞏固學習成果，真正達到解題的目的?！邦}海無邊，總結是岸”是很有道理的。筆者在復習解三角形中，曾有過這樣的經(jīng)歷：在ABC中，證明(a2-b2-c2)tanA+(a2-b2+c2)tanB=0.有的學生給出了如下的證明：設ABC的面積為S，左邊=-2bc cosAtanA+2accosBtanB=-2bcsinA+2acsinB=-4S+4S=0.我首先肯定了這種證法相當巧妙，又不失時機地對學生因勢利導，引導學生對證明結果及過程反思、探索，便易發(fā)現(xiàn)(b2+c2-a2)tanA=(a2+c2-b2)tanB=(a2+b2-c2)tanC=4S; 進一步又有tanA=; tanB=; tanC=; 還有cotA +cotB+cotC=; 等等。這些優(yōu)美和諧的結論反映了學生可貴的創(chuàng)造性思維品質(zhì)。若沒有反思、探索的過程，就題論題，至多就是解了一道題，腦海中不會留下深刻的印象，對解另外的題不會有什么啟發(fā)。在復習中許多學生抱怨說，平時解題甚多，但考試結果卻總不理想。我想造成這種現(xiàn)象的一個重要原因是解題后沒有反思，不善于總結歸納、重新探索，固有的思維成果沒有得到鞏固、提高、升華，思維的創(chuàng)造性沒有得到應有的發(fā)展，導致對知識的遷移能力不夠。