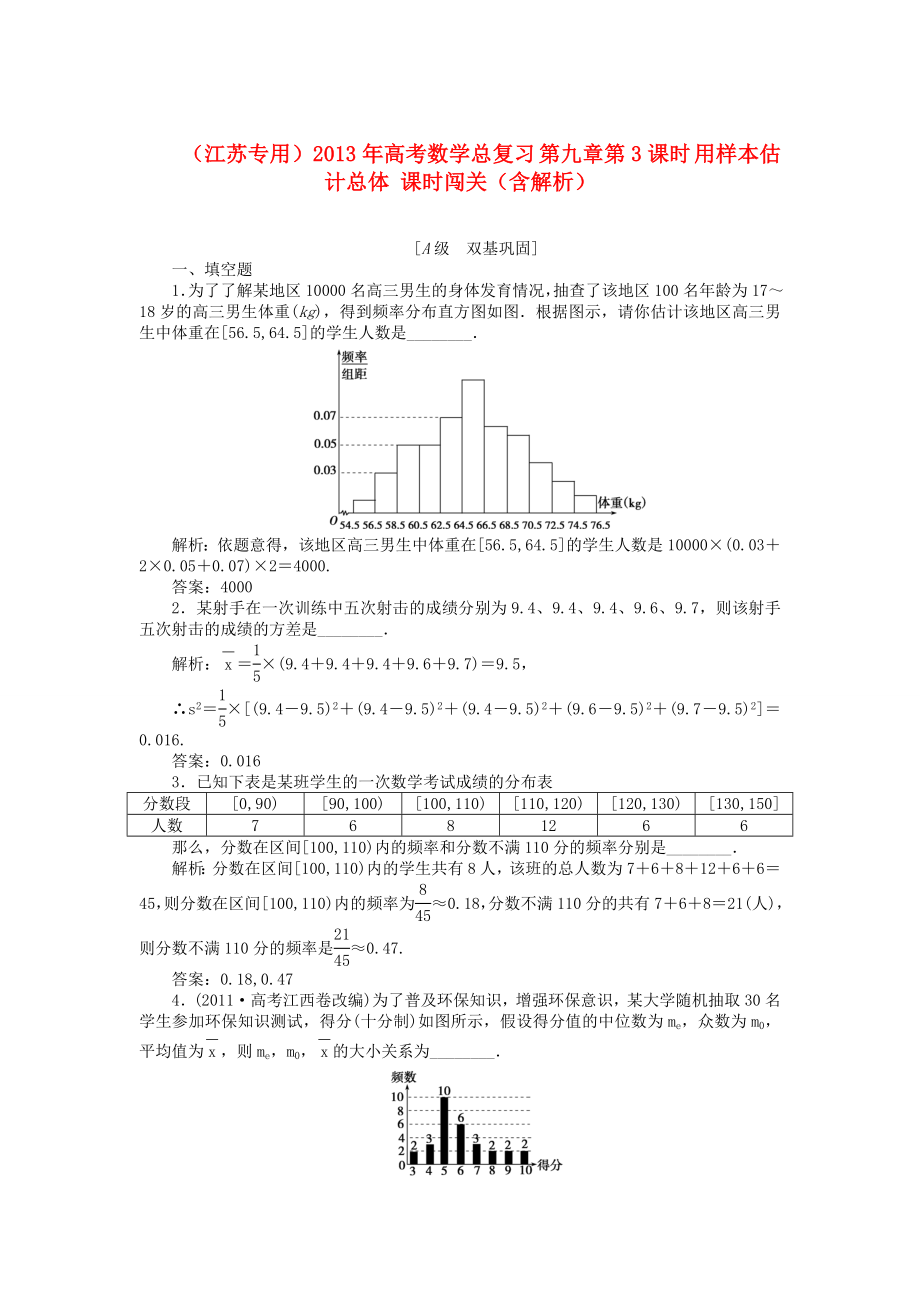
（江蘇專用）2013年高考數(shù)學(xué)總復(fù)習(xí) 第九章第3課時(shí) 用樣本估計(jì)總體 課時(shí)闖關(guān)（含解析）A級(jí)雙基鞏固一、填空題1為了了解某地區(qū)10000名高三男生的身體發(fā)育情況，抽查了該地區(qū)100名年齡為1718歲的高三男生體重(kg)，得到頻率分布直方圖如圖根據(jù)圖示，請(qǐng)你估計(jì)該地區(qū)高三男生中體重在56.5,64.5的學(xué)生人數(shù)是_解析：依題意得，該地區(qū)高三男生中體重在56.5,64.5的學(xué)生人數(shù)是10000×(0.032×0.050.07)×24000.答案：40002某射手在一次訓(xùn)練中五次射擊的成績分別為9.4、9.4、9.4、9.6、9.7，則該射手五次射擊的成績的方差是_解析：×(9.49.49.49.69.7)9.5，s2×(9.49.5)2(9.49.5)2(9.49.5)2(9.69.5)2(9.79.5)20.016.答案：0.0163已知下表是某班學(xué)生的一次數(shù)學(xué)考試成績的分布表分?jǐn)?shù)段0,90)90,100)100,110)110,120)120,130)130,150人數(shù)7681266那么，分?jǐn)?shù)在區(qū)間100,110)內(nèi)的頻率和分?jǐn)?shù)不滿110分的頻率分別是_解析：分?jǐn)?shù)在區(qū)間100,110)內(nèi)的學(xué)生共有8人，該班的總?cè)藬?shù)為768126645，則分?jǐn)?shù)在區(qū)間100,110)內(nèi)的頻率為0.18，分?jǐn)?shù)不滿110分的共有76821(人)，則分?jǐn)?shù)不滿110分的頻率是0.47.答案：0.18,0.474(2011·高考江西卷改編)為了普及環(huán)保知識(shí)，增強(qiáng)環(huán)保意識(shí)，某大學(xué)隨機(jī)抽取30名學(xué)生參加環(huán)保知識(shí)測試，得分(十分制)如圖所示，假設(shè)得分值的中位數(shù)為me，眾數(shù)為m0，平均值為，則me，m0，的大小關(guān)系為_解析：由圖可知，30名學(xué)生的得分情況依次為：2個(gè)人得3分，3個(gè)人得4分，10個(gè)人得5分，6個(gè)人得6分，3個(gè)人得7分，2個(gè)人得8分，2個(gè)人得9分，2個(gè)人得10分中位數(shù)為第15,16個(gè)數(shù)(分別為5,6)的平均數(shù)，即me5.5,5出現(xiàn)次數(shù)最多，故m05，5.97.于是得m0<me<.答案：m0<me<5從甲、乙兩種樹苗中各抽測了10株樹苗的高度，其莖葉圖如圖根據(jù)莖葉圖，下列描述正確的是_甲種樹苗的平均高度大于乙種樹苗的平均高度，且甲種樹苗比乙種樹苗長得整齊甲種樹苗的平均高度大于乙種樹苗的平均高度，但乙種樹苗比甲種樹苗長得整齊乙種樹苗的平均高度大于甲種樹苗的平均高度，且乙種樹苗比甲種樹苗長得整齊乙種樹苗的平均高度大于甲種樹苗的平均高度，但甲種樹苗比乙種樹苗長得整齊解析：根據(jù)莖葉圖計(jì)算得甲種樹苗的平均高度為27，而乙種樹苗的平均高度為30，但乙種樹苗的高度分布不如甲種樹苗的高度分布集中答案：6甲、乙兩名同學(xué)學(xué)業(yè)水平考試的9科成績?nèi)缜o葉圖所示，請(qǐng)你根據(jù)莖葉圖判斷誰的平均分高_(dá)(填“甲”或“乙”)解析：由莖葉圖可以看出，甲(928189×2727378×268)80，乙(918386888972757869)81.2，乙>甲，故乙的平均數(shù)大于甲的平均數(shù)答案：乙7.甲、乙兩名選手參加歌手大賽時(shí)，5名評(píng)委打的分?jǐn)?shù)用莖葉圖表示如圖，s1，s2分別表示甲、乙選手分?jǐn)?shù)的標(biāo)準(zhǔn)差，則s1與s2的大小關(guān)系是_解析：由莖葉圖可得甲84，乙84，所以s22，s62，顯然有s1<s2.答案：s1<s28某校甲、乙兩個(gè)班級(jí)各有編號(hào)為1,2,3,4,5的五名學(xué)生進(jìn)行投籃練習(xí)，每人投10次，投中的次數(shù)如下表：學(xué)生1號(hào)2號(hào)3號(hào)4號(hào)5號(hào)甲班67787乙班67679則以上兩組數(shù)據(jù)的方差中較小一個(gè)為s2，則s2_.解析：甲班的平均數(shù)為甲7，甲班的方差為s；乙班的平均數(shù)為乙7，乙班的方差為s；>，s2.答案：二、解答題9隨機(jī)抽取某中學(xué)甲、乙兩班各10名同學(xué)，測量他們的身高(單位：cm)，獲得身高數(shù)據(jù)的莖葉圖如圖(中間的數(shù)字表示身高的百位、十位數(shù)，旁邊的數(shù)字分別表示身高的個(gè)位數(shù))如圖所示(1)根據(jù)莖葉圖判斷哪個(gè)班的平均身高較高；(2)計(jì)算甲班的樣本方差解：(1)由莖葉圖可知乙班身高比較集中在170181之間，所以乙班的平均身高較高(2)甲班的平均數(shù)為：×(182170171178179162164168168158)170.甲班的方差為：(182170)2(179170)2(178170)2(171170)2(170170)2(168170)2(168170)2(164170)2(162170)2(158170)254.2.10(2012·淄博調(diào)研)從某學(xué)校高三年級(jí)800名學(xué)生中隨機(jī)抽取50名測量身高，被抽取的學(xué)生的身高全部介于155 cm和195 cm之間，將測量結(jié)果按如下方式分成八組：第一組155,160)；第二組160,165)；第八組190,195，如圖是按上述分組方法得到的頻率分布直方圖(1)根據(jù)已知條件填寫下面表格：組別12345678樣本數(shù)(2)估計(jì)這所學(xué)校高三年級(jí)800名學(xué)生中身高在180 cm以上(含180 cm)的人數(shù)解：(1)由頻率分布直方圖得第七組的頻率為：1(0.008×20.016×20.04×20.06)×50.06，第七組的人數(shù)為0.06×503.同理可得各組人數(shù)如下：組別12345678樣本數(shù)24101015432(2)由頻率分布直方圖得后三組的頻率為0.016×50.060.008×50.18.估計(jì)這所學(xué)校高三年級(jí)身高在180 cm以上(含180 cm)的人數(shù)為800×0.18144.B級(jí)能力提升一、填空題1(2011·高考浙江卷)某中學(xué)為了解學(xué)生數(shù)學(xué)課程的學(xué)習(xí)情況，在3000名學(xué)生中隨機(jī)抽取200名，并統(tǒng)計(jì)這200名學(xué)生的某次數(shù)學(xué)考試成績，得到了樣本的頻率分布直方圖(如圖)根據(jù)頻率分布直方圖推測，這3000名學(xué)生在該次數(shù)學(xué)考試中成績小于60分的學(xué)生數(shù)是_解析：由題意知，在該次數(shù)學(xué)考試中成績小于60分的頻率為(0.0020.0060.012)×100.2，故這3000名學(xué)生在該次數(shù)學(xué)考試中成績小于60分的學(xué)生數(shù)是3000×0.2600.答案：6002某地居民的月收入調(diào)查所得數(shù)據(jù)的頻率分布直方圖如圖，居民的月收入的中位數(shù)大約是_元解析：從頻率分布直方圖，可以知道要使得兩邊的面積相等，平分面積的直線應(yīng)該在20002500之間，設(shè)該直線的方程為xa，則500×(0.00020.0004)0.0005×(a2000)0.0005×(2500a)500×(0.00050.00030.0001)，解得a2400，即居民的月收入的中位數(shù)大約是2400.答案：24003某人5次上班途中所花的時(shí)間(單位：分鐘)分別為x，y,10,11,9.已知這組數(shù)據(jù)的平均數(shù)為10，方差為2，則|xy|的值為_解析：由10，得xy20，由(x10)2(y10)20112，得(x10)2(y10)28.故或故|xy|4.答案：44(2012·蘇州質(zhì)檢)設(shè)矩形的長為a，寬為b，其比滿足ba0.618，這種矩形給人以美感，稱為黃金矩形黃金矩形常應(yīng)用于工藝品設(shè)計(jì)中，下面是某工藝品廠隨機(jī)抽取的兩個(gè)批次初加工矩形寬度與長度的比值樣本：甲批次：0.5980.6250.6280.5950.639乙批次：0.6180.6130.5920.6220.620根據(jù)上述兩個(gè)樣本來估計(jì)兩個(gè)批次的總體平均數(shù)，與標(biāo)準(zhǔn)值0.618比較，正確的結(jié)論是_甲批次的總體平均數(shù)與標(biāo)準(zhǔn)值更接近乙批次的總體平均數(shù)與標(biāo)準(zhǔn)值更接近兩個(gè)批次的總體平均數(shù)與標(biāo)準(zhǔn)值接近程度相同兩個(gè)批次的總體平均數(shù)與標(biāo)準(zhǔn)值接近程度不能確定解析：甲0.617，乙0.613，甲與0.618更接近答案：二、解答題5為了研究某高校大學(xué)生新生的視力情況，隨機(jī)地抽查了該校100名進(jìn)校學(xué)生的視力情況，得到頻率分布直方圖，如圖已知前4組頻數(shù)從左到右依次是等比數(shù)列an的前四項(xiàng)，后6組的頻數(shù)從左到右依次是等差數(shù)列bn的前六項(xiàng)(1)求等比數(shù)列an的通項(xiàng)公式；(2)求等差數(shù)列bn的通項(xiàng)公式；(3)若規(guī)定視力低于5.0的學(xué)生屬于近視學(xué)生，試估計(jì)該校新生的近視率的大小解：(1)由題意知a10.1×0.1×1001，a20.3×0.1×1003.數(shù)列an是等比數(shù)列，公比q3，ana1qn13n1.(2)a1a2a313，b1b2b6100(a1a2a3)87.數(shù)列為bn公差為d，則得b1b2b66b115d.6b115d87.b1a427，d5.bn325n.(3)0.91.(或10.91)故估計(jì)該校新生近視率為91%.