《與名師對話高三數(shù)學文一輪復習課時跟蹤訓練：第三章 導數(shù)及其應用 課時跟蹤訓練15 Word版含解析》由會員分享，可在線閱讀，更多相關《與名師對話高三數(shù)學文一輪復習課時跟蹤訓練：第三章 導數(shù)及其應用 課時跟蹤訓練15 Word版含解析（10頁珍藏版）》請在裝配圖網上搜索。

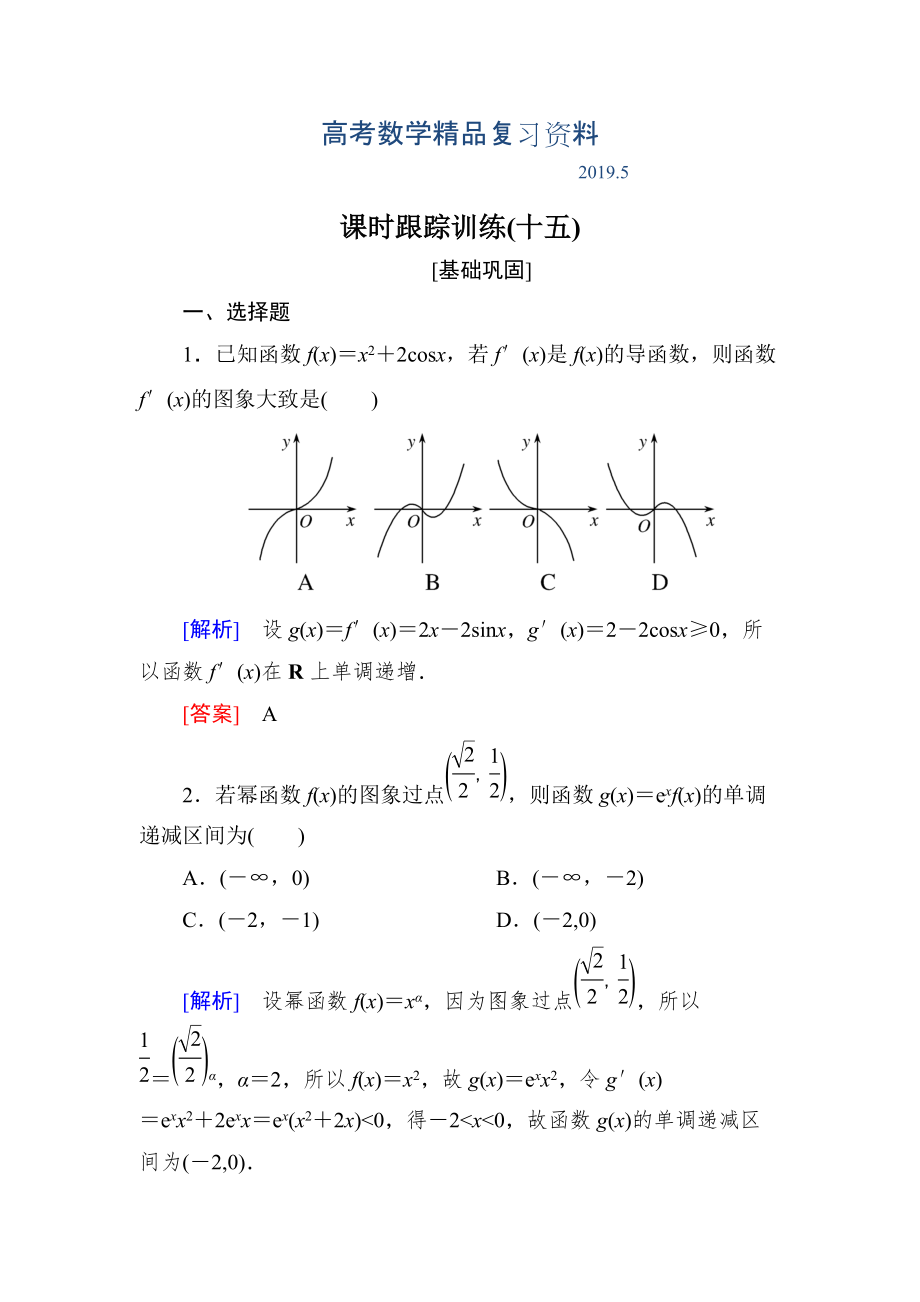
1、 高考數(shù)學精品復習資料 2019.5 課時跟蹤訓練(十五) [基礎鞏固] 一、選擇題 1．已知函數(shù)f(x)＝x2＋2cosx，若f′(x)是f(x)的導函數(shù)，則函數(shù)f′(x)的圖象大致是(　　) [解析]　設g(x)＝f′(x)＝2x－2sinx，g′(x)＝2－2cosx≥0，所以函數(shù)f′(x)在R上單調遞增． [答案]　A 2．若冪函數(shù)f(x)的圖象過點，則函數(shù)g(x)＝exf(x)的單調遞減區(qū)間為(　　) A．(－∞，0) B．(－∞，－2) C．(－2，－1) D．(－2,0) [解析]　設冪函數(shù)

2、f(x)＝xα，因為圖象過點，所以＝α，α＝2，所以f(x)＝x2，故g(x)＝exx2，令g′(x)＝exx2＋2exx＝ex(x2＋2x)<0，得－2<x<0，故函數(shù)g(x)的單調遞減區(qū)間為(－2,0)． [答案]　D 3.如圖所示是函數(shù)f(x)的導函數(shù)f′(x)的圖象，則下列判斷中正確的是(　　) A．函數(shù)f(x)在區(qū)間(－3,0)上是減函數(shù) B．函數(shù)f(x)在區(qū)間(－3,2)上是減函數(shù) C．函數(shù)f(x)在區(qū)間(0,2)上是減函數(shù) D．函數(shù)f(x)在區(qū)間(－3,2)上是單調函數(shù) [解析]　由圖可知，當－3<x<0時，f′(x)<0，所

3、以f(x)在(－3,0)上是減函數(shù)．故選A. [答案]　A 4．函數(shù)f(x)＝2lnx－ax(a>0)的單調遞增區(qū)間為(　　) A. B． C. D．(－∞，a) [解析]　由f′(x)＝－a>0，得0<x<.∴f(x)的單調遞增區(qū)間為.故選A. [答案]　A 5．(20xx·江西臨川一中期中)若函數(shù)f(x)＝x＋alnx不是單調函數(shù)，則實數(shù)a的取值范圍是(　　) A．[0，＋∞) B．(－∞，0] C．(－∞，0) D．(0，＋∞) [解析]　由題意知x>0，f′(x)＝1＋.要使函數(shù)f(x)＝x＋alnx不是單調函數(shù)，則需方程1＋

4、＝0在x>0上有解，所以a<0. [答案]　C 6．(20xx·湖北襄陽模擬)函數(shù)f(x)的定義域為R.f(－1)＝2，對任意x∈R，f′(x)>2，則f(x)>2x＋4的解集為(　　) A．(－1,1) B．(－1，＋∞) C．(－∞，－1) D．(－∞，＋∞) [解析]　由f(x)>2x＋4，得f(x)－2x－4>0.設F(x)＝f(x)－2x－4，則F′(x)＝f′(x)－2.因為f′(x)>2，所以F′(x)>0在R上恒成立，所以F(x)在R上單調遞增，而F(－1)＝f(－1)－2×(－1)－4＝2＋2－4＝

5、0，故不等式f(x)－2x－4>0等價于F(x)>F(－1)，所以x>－1，選B. [答案]　B 二、填空題 7．函數(shù)f(x)＝x2－ax－3在(1，＋∞)上是增函數(shù)，則實數(shù)a的取值范圍是________． [解析]　f′(x)＝2x－a， ∵f(x)在(1，＋∞)上是增函數(shù)， ∴2x－a≥0在(1，＋∞)上恒成立． 即a≤2x，∴a≤2. [答案]　(－∞，2] 8．已知函數(shù)f(x)(x∈R)滿足f(1)＝1，且f(x)的導數(shù)f′(x)<，則不等式f(x2)<＋的解集為________． [解析]　設F(x)＝f(x)－x， ∴F′(x)＝

6、f′(x)－，∵f′(x)<， ∴F′(x)＝f′(x)－<0， 即函數(shù)F(x)在R上單調遞減． ∵f(x2)<＋，∴f(x2)－<f(1)－， ∴F(x2)<F(1)， 而函數(shù)F(x)在R上單調遞減，∴x2>1， 即x∈(－∞，－1)∪(1，＋∞)． [答案]　(－∞，－1)∪(1，＋∞) 9．已知函數(shù)f(x)＝ax－x3，若對區(qū)間(0,1)上的任意x1，x2，且x1<x2，都有f(x2)－f(x1)>x2－x1成立，則實數(shù)a的取值范圍是________． [解析]　問題等價于函數(shù)g(x)＝f(x)－x在區(qū)間(0,1)上為增函

7、數(shù)，即g′(x)＝a－1－3x2≥0，即a≥1＋3x2在(0,1)上恒成立，即a≥4，所以實數(shù)a的取值范圍是[4，＋∞)． [答案]　[4，＋∞) 三、解答題 10．已知函數(shù)f(x)＝＋－lnx－，其中a∈R，且曲線y＝f(x)在點(1，f(1))處的切線垂直于直線y＝x. (1)求a的值； (2)求函數(shù)f(x)的單調區(qū)間． [解]　(1)對f(x)求導得f′(x)＝－－，由f(x)在點(1，f(1))處的切線垂直于直線y＝x知f′(1)＝－－a＝－2，解得a＝. (2)由(1)知f(x)＝＋－lnx－，則f′(x)＝. 令f′(x)＝0，解得x＝－1或x＝5. 因為x＝－1

8、不在f(x)的定義域(0，＋∞)內，故舍去． 當x∈(0,5)時，f′(x)<0， 故f(x)在(0,5)內為減函數(shù)； 當x∈(5，＋∞)時，f′(x)>0， 故f(x)在(5，＋∞)內為增函數(shù)． 綜上，f(x)的單調增區(qū)間為(5，＋∞)，單調減區(qū)間為(0,5)． [能力提升] 11．已知函數(shù)f(x)＝xsinx，x∈R，則f，f(1)，f的大小關系為(　　) A．f>f(1)>f B．f(1)>f>f C．f>f(1)>f D．f>f>f(1) [解析]　由f(－x)＝(－x)sin(－x)＝xsinx＝f(

9、x)，知f(x)是偶函數(shù)． f′(x)＝sinx＋xcosx，當0<x<時，f′(x)>0，所以f(x)在(0，)上為增函數(shù)．又0<<1<<，所以f<f(1)<f.因為f＝f， 所以f>f(1)>f.故選A. [答案]　A 12．(20xx·湖北華北師大附中模擬)若f(x)＝ex＋ae－x為偶函數(shù)，則f(x－1)<的解集為(　　) A．(2，＋∞) B．(0,2) C．(－∞，2) D．(－∞，0)∪(2，＋∞) [解析]　由f(x)＝ex＋ae－x為偶函數(shù)，得f(x)－f(－x)＝(1－a)(ex

10、－e－x)＝0恒成立，所以a＝1，即f(x)＝ex＋e－x，則f′(x)＝ex－e－x.當x∈(－∞，0)時，f′(x)<0；x∈(0，＋∞)時，f′(x)>0，即f(x)在(－∞，0)上單調遞減，在(0，＋∞)上單調遞增，且圖象關于y軸對稱．由f(x－1)<＝f(1)得|x－1|<1，解得0<x<2，即f(x－1)<的解集為(0,2)，故選B. [答案]　B 13．(20xx·福建福州質檢)已知函數(shù)f(x)＝alnx＋x2＋(a－6)x在(0,3)上不是單調函數(shù)，則實數(shù)a的取值范圍是________． [解析]　f′(x)＝＋2x＋a

11、－6＝(x>0)． 設g(x)＝2x2＋(a－6)x＋a(x>0)， 因為函數(shù)f(x)在(0,3)上不是單調函數(shù)， 等價于函數(shù)g(x)＝2x2＋(a－6)x＋a(x>0)在(0,3)上不會恒大于零或恒小于零． 又g(0)＝a，g(3)＝4a，所以 解得0<a<2， 所以實數(shù)a的取值范圍為(0,2)． [答案]　(0,2) 14．(20xx·山東卷)若函數(shù)exf(x)(e＝2.71828…是自然對數(shù)的底數(shù))在f(x)的定義域上單調遞增，則稱函數(shù)f(x)具有M性質．下列函數(shù)中所有具有M性質的函數(shù)的序號為________． ①f(x)＝2－x

12、；②f(x)＝3－x；③f(x)＝x3；④f(x)＝x2＋2. [解析]?、僖驗閒(x)＝2－x的定義域為R，又exf(x)＝ex·2－x＝x在R上單調遞增，故f(x)＝2－x具有M性質． ②因為f(x)＝3－x的定義域為R，又exf(x)＝ex·3－x＝x在R上單調遞減，故f(x)＝3－x不具有M性質． ③因為f(x)＝x3的定義域為R，又exf(x)＝ex·x3，構造函數(shù)g(x)＝ex·x3，則g′(x)＝ex·x3＋ex·3x2＝x2ex(x＋3)，當x>－3時，g′(x)>0，當x<－3時，g′(x)&

13、lt;0，所以exf(x)＝ex·x3在(－∞，－3)上單調遞減，在(－3，＋∞)上單調遞增，故f(x)＝x3不具有M性質． ④因為f(x)＝x2＋2的定義域為R，又exf(x)＝ex(x2＋2)，構造函數(shù)h(x)＝ex(x2＋2)，則h′(x)＝ex(x2＋2)＋ex·2x＝ex[(x＋1)2＋1]>0，所以exf(x)＝ex(x2＋2)在R上單調遞增，故f(x)＝x2＋2具有M性質．故填①④. [答案]?、佗? 15．(20xx·全國卷Ⅱ改編)已知函數(shù)f(x)＝lnx＋a(1－x)． (1)討論f(x)的單調性； (2)若f(x)在(2，＋∞)上

14、為單調函數(shù)，求實數(shù)a的取值范圍． [解]　(1)f(x)的定義域為(0，＋∞)，f′(x)＝－a.若a≤0，則f′(x)>0，f(x)在(0，＋∞)上單調遞增；若a>0，則當x∈時，f′(x)>0；當x∈時，f′(x)<0，所以f(x)在上單調遞增，在上單調遞減． ∴綜上當a≤0時f(x)在(0，＋∞)單調遞增． 當a>0時f(x)在單調遞增，在單調遞減． (2)由(1)知，當a≤0時，f(x)在(0，＋∞)上單調遞增，符合要求；當a>0時，f(x)在上單調遞減，則2≥，即a≥.∴實數(shù)a的取值范圍是(－∞，0]∪. 16．(20xx·全國

15、卷Ⅰ)已知函數(shù)f(x)＝(x－2)ex＋a(x－1)2.討論f(x)的單調性． [解]　f′(x)＝(x－1)ex＋2a(x－1)＝(x－1)(ex＋2a)． (ⅰ)設a≥0，則當x∈(－∞，1)時，f′(x)<0；當x∈(1，＋∞)時，f′(x)>0，所以f(x)在(－∞，1)上單調遞減，在(1，＋∞)上單調遞增． (ⅱ)設a<0，由f′(x)＝0得x＝1或x＝ln(－2a)． ①若a＝－，則f′(x)＝(x－1)(ex－e)，所以f(x)在(－∞，＋∞)單調遞增． ②若a>－，則ln(－2a)<1，故當x∈(－∞，ln(－2a))∪(1，＋∞)時，f

16、′(x)>0；當x∈(ln(－2a)，1)時，f′(x)<0，所以f(x)在(－∞，ln(－2a))，(1，＋∞)上單調遞增，在(ln(－2a)，1)上單調遞減． ③若a<－，則ln(－2a)>1，故當x∈(－∞，1)∪(ln(－2a)，＋∞)時，f′(x)>0；當x∈(1，ln(－2a))時，f′(x)<0，所以f(x)在(－∞，1)，(ln(－2a)，＋∞)上單調遞增，在(1，ln(－2a))上單調遞減． [延伸拓展] 　已知函數(shù)f(x)＝－2x2＋lnx(a>0)．若函數(shù)f(x)在[1,2]上為單調函數(shù)，則a的取值范圍是________． [解析]　f′(x)＝－4x＋，若函數(shù)f(x)在[1,2]上為單調函數(shù)，即f′(x)＝－4x＋≥0或f′(x)＝－4x＋≤0在[1,2]上恒成立即≥4x－或≤4x－在[1,2]上恒成立．令h(x)＝4x－，則h(x)在[1,2]上單調遞增，所以≥h(2)或≤h(1)，即≥或≤3，又a>0，所以0<a≤或a≥1. [答案]　∪[1，＋∞)