《新編高考數(shù)學(xué)復(fù)習(xí):第七章 :第二節(jié)空間幾何體的表面積和體積突破熱點(diǎn)題型》由會(huì)員分享�,可在線閱讀�,更多相關(guān)《新編高考數(shù)學(xué)復(fù)習(xí):第七章 :第二節(jié)空間幾何體的表面積和體積突破熱點(diǎn)題型(6頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1�、新編高考數(shù)學(xué)復(fù)習(xí)資料
第二節(jié) 空間幾何體的表面積和體積
考點(diǎn)一
空間幾何體的表面積
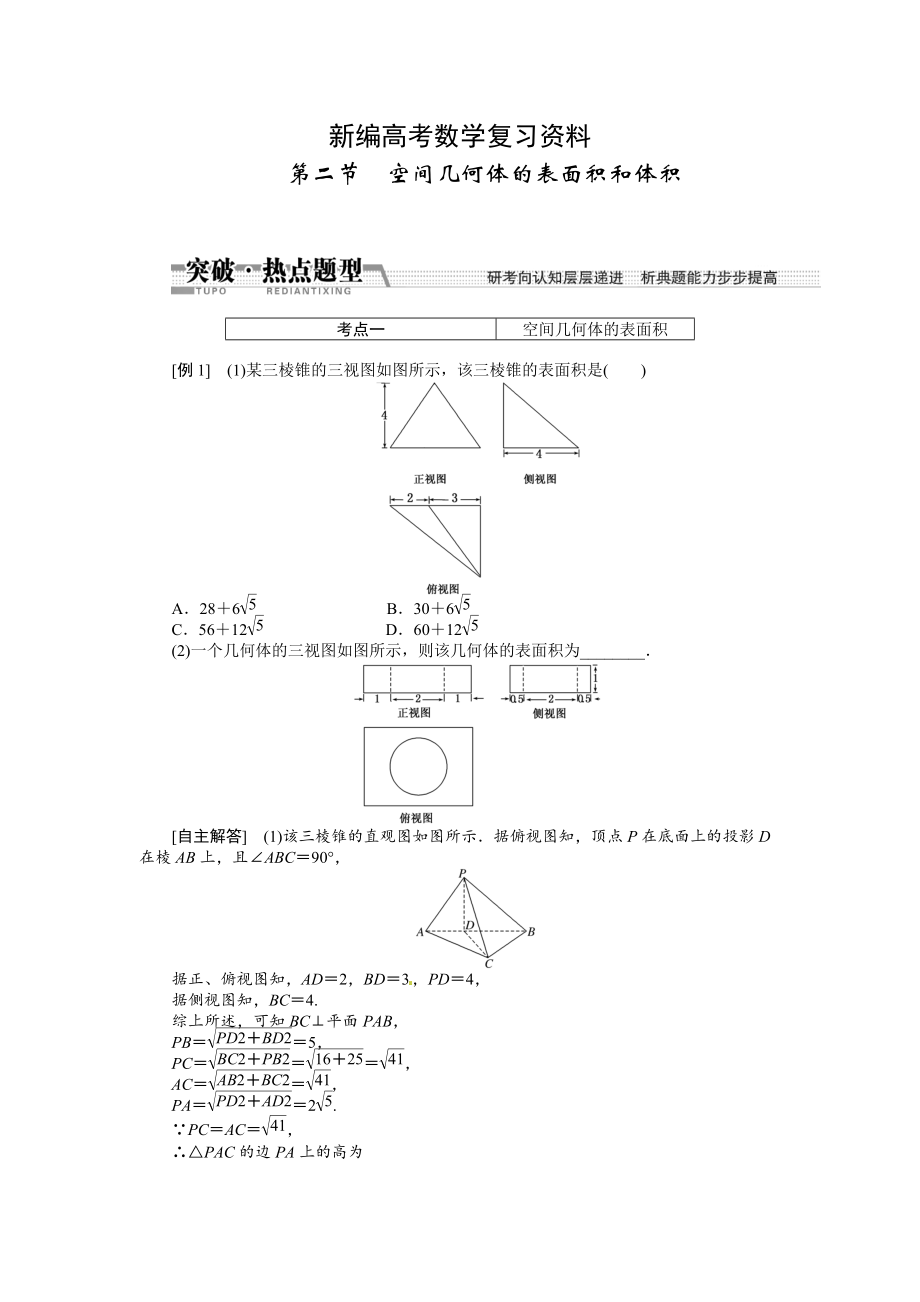
[例1] (1)某三棱錐的三視圖如圖所示�,該三棱錐的表面積是( )
A.28+6 B.30+6
C.56+12 D.60+12
(2)一個(gè)幾何體的三視圖如圖所示,則該幾何體的表面積為________.
[自主解答] (1)該三棱錐的直觀圖如圖所示.據(jù)俯視圖知,頂點(diǎn)P在底面上的投影D在棱AB上,且∠ABC=90°�,[來(lái)源:]
據(jù)正�、俯視圖知�,AD=2�,BD=3�,PD=4�,
據(jù)側(cè)視圖知,BC=4
2�、.
綜上所述�,可知BC⊥平面PAB,
PB==5�,
PC===,
AC==,
PA==2.
∵PC=AC=�,
∴△PAC的邊PA上的高為
h= =6.
∴S△PAB=AB·PD=10,S△ABC=AB·BC=10�,
S△PBC=PB·BC=10,S△APC=PA·h=6.
故三棱錐的表面積為
S△PAB+S△ABC+S△PBC+S△APC=30+6.
(2)該幾何體的直觀圖如圖所示:
該幾何體為長(zhǎng)為4�,寬為3,高為1的長(zhǎng)方體內(nèi)部挖去一個(gè)底面半徑為1,高為1的圓柱.
∴S表=2×(4+3+12)+2π-2π=38.
[答案] (1)B (2)38
3、
【方法規(guī)律】
空間幾何體的表面積的求法技巧
(1)多面體的表面積是各個(gè)面的面積之和;組合體的表面積應(yīng)注意重合部分的處理.
(2)圓柱、圓錐、圓臺(tái)的側(cè)面是曲面�,計(jì)算側(cè)面積時(shí)需要將這個(gè)曲面展為平面圖形計(jì)算�,而表面積是側(cè)面積與底面圓的面積之和.
一個(gè)幾何體的三視圖如圖所示�,該幾何體的表面積是( )
A.372 B.360 C.292 D.280
解析:選B 由三視圖可知該幾何體是由下面一個(gè)長(zhǎng)方體,上面一個(gè)長(zhǎng)方體組合而成的幾何體.
∵下面長(zhǎng)方體的表面積為8×10×2+2×8×2+10×2×2=232,上面長(zhǎng)方體的表面積為8×6×2+2×
4�、8×2+2×6×2=152�,
又∵長(zhǎng)方體表面積重疊一部分�,
∴幾何體的表面積為232+152-2×6×2=360.
高頻考點(diǎn)
考點(diǎn)二 空間幾何體的體積
1.空間幾何體的體積是每年高考的熱點(diǎn)�,題型既有選擇題、填空題�,也有解答題,難度偏小�,屬容易題.
2.高考對(duì)空間幾何體的體積的考查常有以下幾個(gè)命題角度:
(1)求簡(jiǎn)單幾何體的體積;
(2)求組合體的體積�;
(3)求以三視圖為背景的幾何體的體積.
[例2] (1)(2013·湖北高考)一個(gè)幾何體的三視圖如圖所示,該幾何體從上到下由四個(gè)簡(jiǎn)單幾何體組成�,其體積分別記為V1,V2�,V3,V4�,上面兩個(gè)簡(jiǎn)單幾何體均
5、為旋轉(zhuǎn)體�,下面兩個(gè)簡(jiǎn)單幾何體均為多面體,則有( )
A.V1<V2<V4<V3 B.V1<V3<V2<V4
C.V2<V1<V3<V4 D.V2<V3<V1<V4
(2)(2013·浙江高考)已知某幾何體的三視圖(單位:cm)如圖所示�,則該幾何體的體積是( )
A.108 cm3 B.100 cm3
C.92 cm3 D.84 cm3
(3)(2012·江蘇高考)如圖所示,在長(zhǎng)方體ABCD -A1B1C1D1中�,AB=AD=3 cm,AA1=2 cm�,則四棱錐A-BB
6、1D1D的體積為________cm3.
[自主解答] (1)由題意可知�,由于上面兩個(gè)簡(jiǎn)單幾何體均為旋轉(zhuǎn)體,下面兩個(gè)簡(jiǎn)單幾何體均為多面體.根據(jù)三視圖可知�,最上面一個(gè)簡(jiǎn)單幾何體是上底面圓的半徑為2,下底面圓的半徑為1�,高為1的圓臺(tái)�,其體積V1=π×(12+22+1×2)×1=π�;從上到下的第二個(gè)簡(jiǎn)單幾何體是一個(gè)底面圓半徑為1,高為2的圓柱�,其體積V2=π×12×2=2π�;從上到下的第三個(gè)簡(jiǎn)單幾何體是邊長(zhǎng)為2的正方體,其體積V3=23=8�;從上到下的第四個(gè)簡(jiǎn)單幾何體是一個(gè)棱臺(tái),其上底面是邊長(zhǎng)為2的正方形�,下底面是邊長(zhǎng)為4的正方形,棱臺(tái)的高為1�,故體積V4=×(22+2×4+42)×1=,比較
7�、大小可知答案選C.
(2)根據(jù)幾何體的三視圖可知,所求幾何體是一個(gè)長(zhǎng)方體截去一個(gè)三棱錐�,則幾何體的體積V=6×6×3-××4×4×3=100 cm3.
(3)由題意,四邊形ABCD為正方形�,連接AC,交BD于O�,則AC⊥BD.由面面垂直的性質(zhì)定理,可證AO⊥平面BB1D1D.四棱錐底面BB1D1D的面積為3×2=6�,從而VA-BB1D1D=×OA×S長(zhǎng)方形BB1D1D=6.
[答案] (1)C (2)B (3)6
空間幾何體體積問(wèn)題的常見類型及解題策略
(1)求簡(jiǎn)單幾何體的體積.若所給的幾何體為柱體、錐體或臺(tái)體�,則可直接利用公式求解.
(2)求組合體的體積.若所給定的幾何體是組
8、合體�,不能直接利用公式求解�,則常用轉(zhuǎn)換法�、分割法、補(bǔ)形法等進(jìn)行求解.
(3)求以三視圖為背景的幾何體的體積.應(yīng)先根據(jù)三視圖得到幾何體的直觀圖�,然后根據(jù)條件求解.
1.(2013·廣東高考)某四棱臺(tái)的三視圖如圖所示,則該四棱臺(tái)的體積是( )
A.4 B. C. D.6
解析:選B 由四棱臺(tái)的三視圖可知�,臺(tái)體上底面積S1=1×1=1,下底面積S2=2×2=4�,高h(yuǎn)=2,代入臺(tái)體的體積公式V=(S1++S2)h=×(1++4)×2=.
2.一幾何體的三視圖如圖所示�,則該幾何體的體積為( )
A.200+9π
9、 B.200+18π
C.140+9π D.140+18π
解析:選A 這個(gè)幾何體由上�、下兩部分組成,下半部分是一個(gè)長(zhǎng)方體�,其中長(zhǎng)、寬�、高分別為6+2+2=10,1+2+1=4,5;上半部分是一個(gè)橫放的半圓柱�,其中底面半徑為=3,母線長(zhǎng)為2�,故V=10×4×5+π×32×2=200+9π.
考點(diǎn)三
與球有關(guān)的組合體
[例3] (2014·沈陽(yáng)模擬)已知直三棱柱ABC-A1B1C1的6個(gè)頂點(diǎn)都在球O的球面上,若AB=3�,AC=4,AB⊥AC�,AA1=12,則球O的半徑為( )
A. B.2 C.
10�、 D.3
[自主解答] 如圖所示�,由球心作平面ABC的垂線�,則垂足為BC的中點(diǎn)M.
又AM=BC=,OM=AA1=6�,
所以球O的半徑R=OA= =.
[答案] C
【互動(dòng)探究】[來(lái)源:]
側(cè)棱和底面邊長(zhǎng)都是3的正四棱錐的外接球半徑是多少?
解:依題意得�,該正四棱錐的底面對(duì)角線的長(zhǎng)為3×=6,高為 =3�,
因此底面中心到各頂點(diǎn)的距離均等于3,
所以該四棱錐的外接球的球心即為底面正方形的中心�,其外接球的半徑為3.
【方法規(guī)律】
與球有關(guān)的組合體的類型及解法
(1)球與旋轉(zhuǎn)體的組合通常作出它們的軸截面解題.
(2)球與多面體的組合�,通常過(guò)多面體
11、的一條側(cè)棱和球心�,或“切點(diǎn)”、“接點(diǎn)”作出截面圖�,把空間問(wèn)題化歸為平面問(wèn)題.
(2013·新課標(biāo)全國(guó)卷Ⅰ)如圖所示,有一個(gè)水平放置的透明無(wú)蓋的正方體容器�,容器高8 cm,將一個(gè)球放在容器口�,再向容器內(nèi)注水,當(dāng)球面恰好接觸水面時(shí)測(cè)得水深為6 cm�,如果不計(jì)容器厚度,則球的體積為( )
A. cm3 B. cm3
C. cm3 D. cm3
解析:選A 設(shè)球半徑為R cm�,根據(jù)已知條件知正方體的上底面與球相交所得截面圓的半徑為4 cm,球心到截面的距離為(R-2)cm�,所以由42+(R-2)2=R2�,得R=5�,所以球的體積
12、V=πR3=π×53= cm3.
——————————[課堂歸納——通法領(lǐng)悟]————————————————
1種思想——轉(zhuǎn)化與化歸思想
計(jì)算旋轉(zhuǎn)體的側(cè)面積時(shí)�,一般采用轉(zhuǎn)化的方法來(lái)進(jìn)行,即將側(cè)面展開化為平面圖形�,“化曲為直”來(lái)解決,因此要熟悉常見旋轉(zhuǎn)體的側(cè)面展開圖的形狀及平面圖形面積的求法.[來(lái)源:]
2種方法——割補(bǔ)法與等積法
(1)割補(bǔ)法:求一些不規(guī)則幾何體的體積時(shí)�,常用割補(bǔ)法轉(zhuǎn)化成已知體積公式的幾何體進(jìn)行解決.
(2)等積法:等積法包括等面積法和等體積法.等積法的前提是幾何圖形(或幾何體)的面積(或體積)通過(guò)已知條件可以得到,利用等積法可以用來(lái)求解幾何圖形的高或幾何體的高�,特別是在求三角形的高和三棱錐的高時(shí),這一方法回避了通過(guò)具體作圖得到三角形(或三棱錐)的高�,而通過(guò)直接計(jì)算得到高的數(shù)值.
2個(gè)注意點(diǎn)——求空間幾何體的表面積應(yīng)注意兩點(diǎn)
(1)求組合體的表面積時(shí),要注意各幾何體重疊部分的處理.[來(lái)源:]
(2)底面是梯形的四棱柱側(cè)放時(shí)�,容易和四棱臺(tái)混淆,在識(shí)別時(shí)要緊扣定義�,以防出錯(cuò).
 新編高考數(shù)學(xué)復(fù)習(xí):第七章 :第二節(jié)空間幾何體的表面積和體積突破熱點(diǎn)題型
新編高考數(shù)學(xué)復(fù)習(xí):第七章 :第二節(jié)空間幾何體的表面積和體積突破熱點(diǎn)題型