《山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 隨堂演練 第六章 圓 第一節(jié) 圓的有關(guān)概念及性質(zhì)試題》由會(huì)員分享，可在線閱讀，更多相關(guān)《山東省濟(jì)南市2018年中考數(shù)學(xué)一輪復(fù)習(xí) 隨堂演練 第六章 圓 第一節(jié) 圓的有關(guān)概念及性質(zhì)試題（4頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

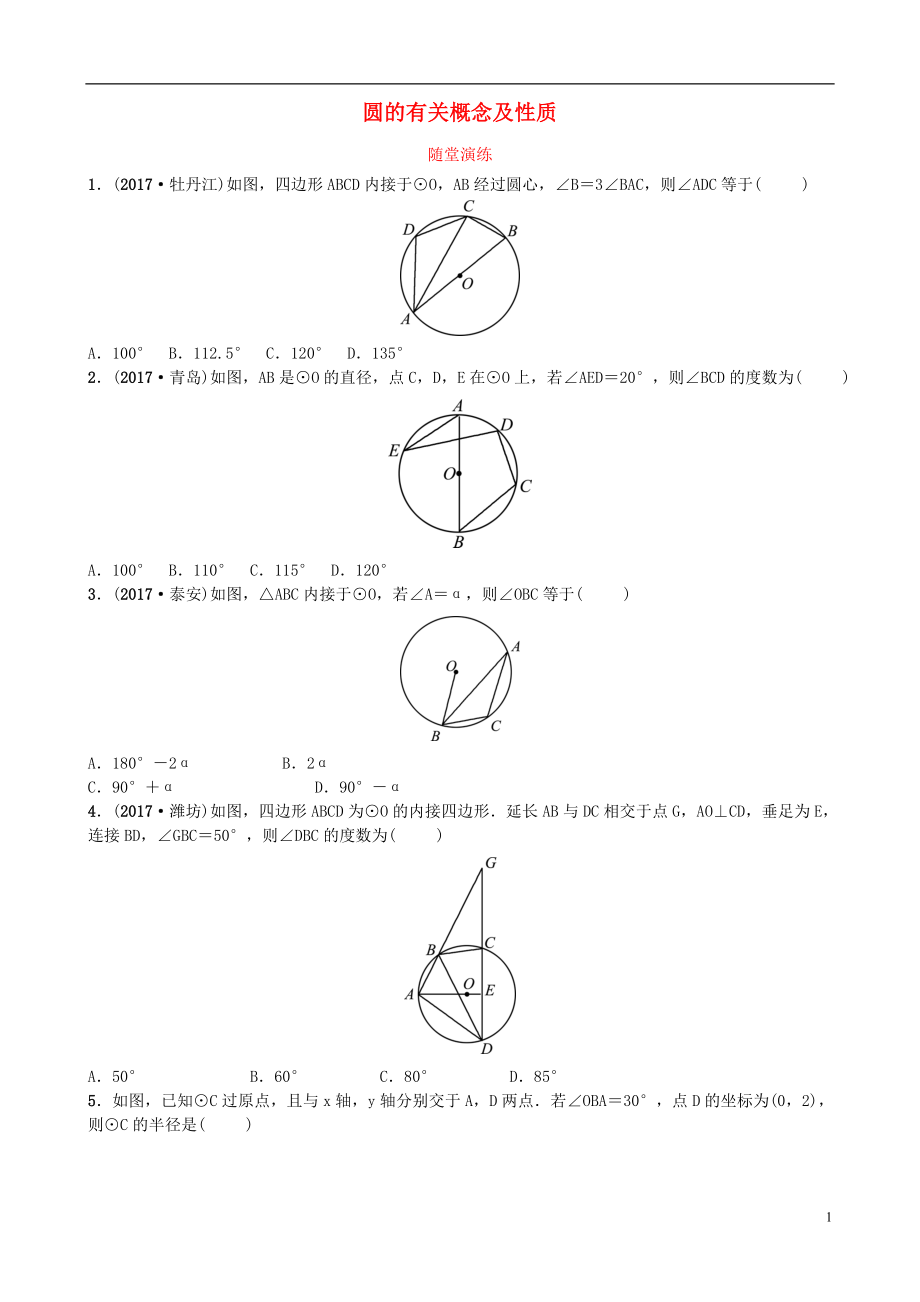
1、 圓的有關(guān)概念及性質(zhì) 隨堂演練 1．(2017·牡丹江)如圖，四邊形ABCD內(nèi)接于⊙O，AB經(jīng)過(guò)圓心，∠B＝3∠BAC，則∠ADC等于( ) A．100° B．112.5° C．120° D．135° 2．(2017·青島)如圖，AB是⊙O的直徑，點(diǎn)C，D，E在⊙O上，若∠AED＝20°，則∠BCD的度數(shù)為( ) A．100° B．110° C．115° D．120° 3．(2017·泰安)如圖，△ABC內(nèi)接于⊙O，若∠A＝α，則∠OBC等于( ) A．180°－2α B．2α C．90°＋α D．90°－α

2、 4．(2017·濰坊)如圖，四邊形ABCD為⊙O的內(nèi)接四邊形．延長(zhǎng)AB與DC相交于點(diǎn)G，AO⊥CD，垂足為E，連接BD，∠GBC＝50°，則∠DBC的度數(shù)為( ) A．50° B．60° C．80° D．85° 5．如圖，已知⊙C過(guò)原點(diǎn)，且與x軸，y軸分別交于A，D兩點(diǎn)．若∠OBA＝30°，點(diǎn)D的坐標(biāo)為(0，2)，則⊙C的半徑是( ) A. B. C．4 D．2 6．如圖，圓內(nèi)接四邊形ABCD中兩組對(duì)邊的延長(zhǎng)線分別相交于點(diǎn)E，F(xiàn)，且∠A＝55°，∠E＝30°，則∠F＝__________． 7．如圖，水平放置的圓柱

3、形排水管道的截面直徑是1 m，其中水面的寬AB為0.8 m，則排水管內(nèi)水的深度為__________m. 8．如圖，四邊形ABCD是⊙O的內(nèi)接四邊形，BC的延長(zhǎng)線與AD的延長(zhǎng)線交于點(diǎn)E，且DC＝DE. (1)求證：∠A＝∠AEB； (2)連接OE，交CD于點(diǎn)F，OE⊥CD，求證：△ABE是等邊三角形． 9．(2017·臨沂)如圖，∠BAC的平分線交△ABC的外接圓于點(diǎn)D，∠ABC的平分線交AD于點(diǎn)E. (1)求證：DE＝DB； (2)若∠BAC＝90°，BD＝4，求△ABC外接圓的半徑． 參考答案 1．B　

4、2.B　3.D　4.C　5.B　6.40°　7.0.8 8．證明：(1)∵四邊形ABCD是⊙O的內(nèi)接四邊形， ∴∠A＋∠BCD＝180°. ∵∠DCE＋∠BCD＝180°，∴∠A＝∠DCE. ∵DC＝DE，∴∠AEB＝∠DCE， ∴∠A＝∠AEB. (2)∵∠A＝∠AEB，∴△ABE是等腰三角形． ∵EO⊥CD，∴CF＝DF， ∴EO是CD的垂直平分線，∴ED＝EC. ∵DC＝DE，∴DC＝DE＝EC， ∴△DCE是等邊三角形，∴∠AEB＝60°， ∴△ABE是等邊三角形． 9．(1)證明：∵AD平分∠BAC，BE平分∠ABC， ∴∠BAD＝∠CAD，∠ABE＝∠CBE. 又∵∠BED＝∠ABE＋∠BAD， ∠DBE＝∠DBC＋∠CBE，∠DBC＝∠DAC， ∴∠BED＝∠DBE，∴DE＝DB. (2)解：如圖，連接CD. ∵∠BAC＝90°， ∴BC是圓的直徑， ∴∠BDC＝90°. ∵∠BAD＝∠CAD， ∴＝，∴BD＝CD， ∴△BCD是等腰直角三角形． ∵BD＝4，∴BC＝4， ∴△ABC的外接圓的半徑為2. 4