《2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計(jì) 第二板塊 熱點(diǎn)問題突破 專題1 圖表信息專題提升演練 新人教版》由會(huì)員分享����,可在線閱讀���,更多相關(guān)《2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計(jì) 第二板塊 熱點(diǎn)問題突破 專題1 圖表信息專題提升演練 新人教版(3頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
1���、專題一 圖表信息
專題提升演練
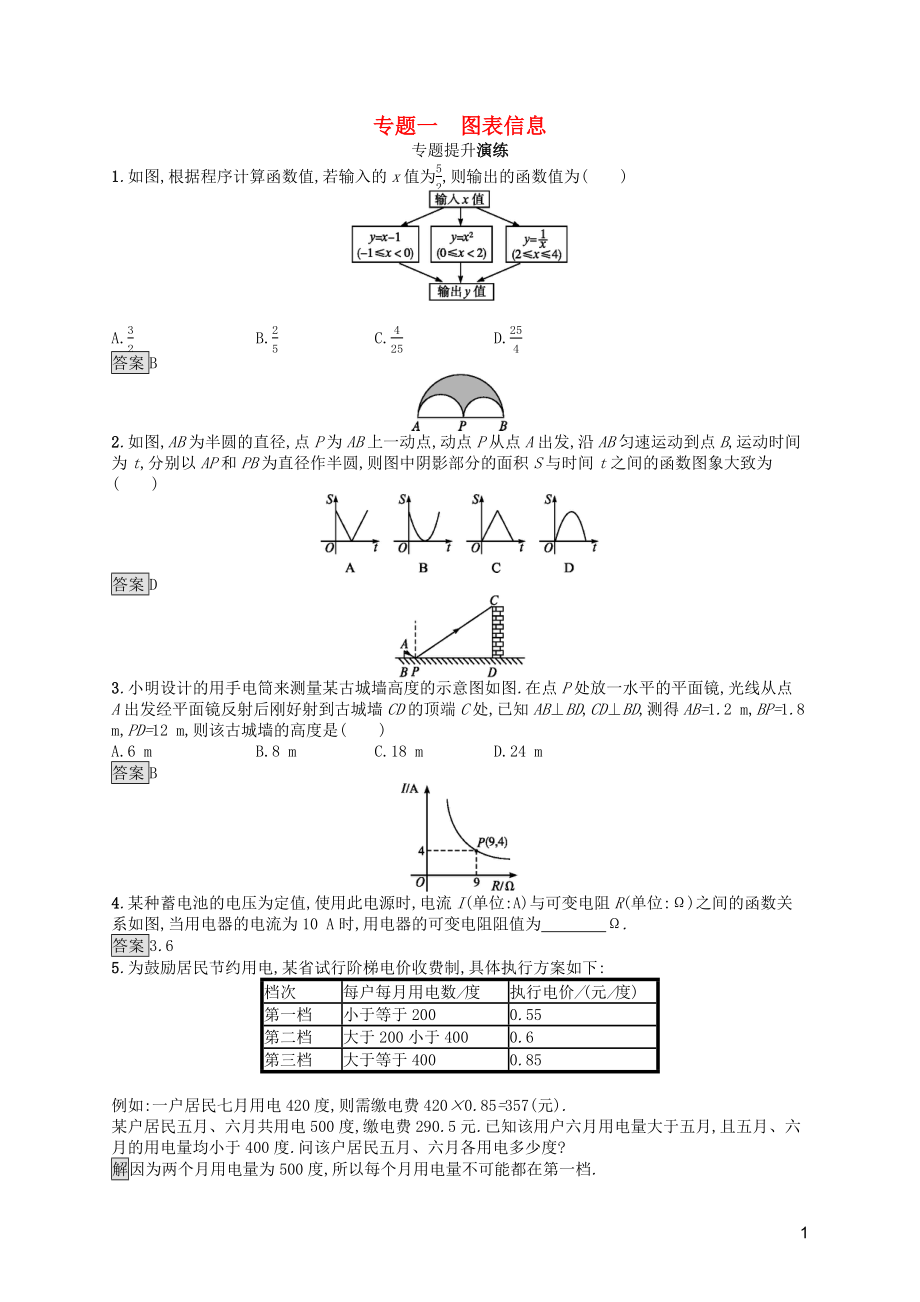
1.如圖,根據(jù)程序計(jì)算函數(shù)值,若輸入的x值為52,則輸出的函數(shù)值為( )
A.32 B.25 C.425 D.254
答案B
2.如圖,AB為半圓的直徑,點(diǎn)P為AB上一動(dòng)點(diǎn),動(dòng)點(diǎn)P從點(diǎn)A出發(fā),沿AB勻速運(yùn)動(dòng)到點(diǎn)B,運(yùn)動(dòng)時(shí)間為t,分別以AP和PB為直徑作半圓,則圖中陰影部分的面積S與時(shí)間t之間的函數(shù)圖象大致為( )
答案D
3.小明設(shè)計(jì)的用手電筒來測(cè)量某古城墻高度的示意圖如圖.在點(diǎn)P處放一水平的平面鏡,光線從點(diǎn)A出發(fā)經(jīng)平面鏡反射后剛好射到古城墻CD的頂端C處,已知AB⊥BD,CD⊥BD,測(cè)得AB
2�����、=1.2 m,BP=1.8 m,PD=12 m,則該古城墻的高度是( )
A.6 m B.8 m C.18 m D.24 m
答案B
4.某種蓄電池的電壓為定值,使用此電源時(shí),電流I(單位:A)與可變電阻R(單位:Ω)之間的函數(shù)關(guān)系如圖,當(dāng)用電器的電流為10 A時(shí),用電器的可變電阻阻值為 Ω.?
答案3.6
5.為鼓勵(lì)居民節(jié)約用電,某省試行階梯電價(jià)收費(fèi)制,具體執(zhí)行方案如下:
檔次
每戶每月用電數(shù)/度
執(zhí)行電價(jià)/(元/度)
第一檔
小于等于200
0.55
第二檔
大于200小于400
0.6
第三檔
大于等于400
0.85
例如:一戶居民七
3�、月用電420度,則需繳電費(fèi)420×0.85=357(元).
某戶居民五月�、六月共用電500度,繳電費(fèi)290.5元.已知該用戶六月用電量大于五月,且五月、六月的用電量均小于400度.問該戶居民五月����、六月各用電多少度?
解因?yàn)閮蓚€(gè)月用電量為500度,所以每個(gè)月用電量不可能都在第一檔.
假設(shè)該用戶五月、六月每月用電均超過200度,
此時(shí)的電費(fèi)共計(jì):500×0.6=300(元),
而300>290.5,不符合題意.
又因?yàn)榱掠秒娏看笥谖逶?所以五月用電量在第一檔,六月用電量在第二檔.
設(shè)五月用電x度,六月用電y度,
根據(jù)題意,得0.55x+0.6y=290.5,x+y=500,解得x
4����、=190,y=310.
故該戶居民五月、六月各用電190度�、310度.
6.在一次中學(xué)生田徑運(yùn)動(dòng)會(huì)上,根據(jù)參加男子跳高初賽的運(yùn)動(dòng)員的成績(jī)(單位:m),繪制出如下的統(tǒng)計(jì)圖①和圖②.請(qǐng)根據(jù)相關(guān)信息,解答下列問題:
圖①
圖②
(1)圖①中a的值為 ;?
(2)求統(tǒng)計(jì)的這組初賽成績(jī)數(shù)據(jù)的平均數(shù)、眾數(shù)和中位數(shù).
解(1)25
(2)∵x=1.50×2+1.55×4+1.60×5+1.65×6+1.70×32+4+5+6+3=1.61,
∴這組數(shù)據(jù)的平均數(shù)是1.61.
∵在這組數(shù)據(jù)中,1.65出現(xiàn)了6次,出現(xiàn)的次數(shù)最多,
∴這組數(shù)據(jù)的眾數(shù)為1.65.
∵將
5���、這組數(shù)據(jù)按從小到大的順序排列,其中處于中間的兩個(gè)數(shù)都是1.60,又1.60+1.602=1.60,
∴這組數(shù)據(jù)的中位數(shù)為1.60.
7.實(shí)驗(yàn)數(shù)據(jù)顯示,一般成人喝半斤低度白酒后,1.5時(shí)內(nèi)其血液中酒精含量y(單位:毫克/百毫升)與時(shí)間x(單位:時(shí))的關(guān)系可近似地用二次函數(shù)y=-200x2+400x刻畫;1.5時(shí)后(包括1.5時(shí))的y與x可近似地用反比例函數(shù)y=kx(k>0)刻畫(如圖).
(1)根據(jù)上述數(shù)學(xué)模型計(jì)算:
①喝酒后幾時(shí)血液中的酒精含量達(dá)到最大值?最大值為多少?
②當(dāng)x=5時(shí),y=45,求k的值.
(2)按國家規(guī)定,車輛駕駛?cè)藛T血液中的酒精含量大于或等于20毫克/百毫升時(shí)屬于“酒后駕駛”,不能駕車上路.參照上述數(shù)學(xué)模型,假設(shè)某駕駛員晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否駕車去上班?請(qǐng)說明理由.
解(1)①當(dāng)x=-b2a=-4002×(-200)=1時(shí),y取得最大值,此時(shí)y=200.
所以喝酒后1時(shí)血液中的酒精含量達(dá)到最大值,最大值為200毫克/百毫升.
②把x=5,y=45代入反比例函數(shù)y=kx,解得k=225.
(2)把y=20代入反比例函數(shù)y=225x,解得x=11.25.
喝完酒經(jīng)過11.25時(shí)為第二天早上7:15.
所以第二天早上7:15以后才可以駕車,7:00不能駕車去上班.
3
 2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計(jì) 第二板塊 熱點(diǎn)問題突破 專題1 圖表信息專題提升演練 新人教版
2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計(jì) 第二板塊 熱點(diǎn)問題突破 專題1 圖表信息專題提升演練 新人教版